Resources Math 3 Course Home Page Math 3 Course Syllabus Practice Exams Textbook Home Page Post a Comment

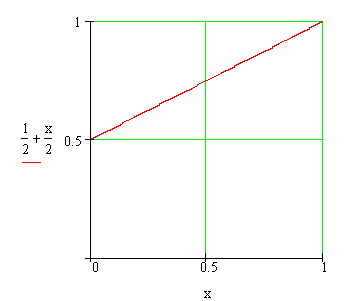
Contents In this lecture we state and prove the Fundamental Theorem of Calculus. This theorem has that name because it relates derivatives and integrals, the two main branches of calculus. We also discuss some resulting techniques for evaluating definite integrals. Quick Question What is the area under the graph of f(x) = 1/2 + x/2 and above the interval [0,1]? Now let F(x) = x/2 + x2/4; what is F(1) − F(0)? Answer Outline Outlines for The Fundamental Theorem of Calculus Techniques of Integration Textbook The Fundamental Theorem of Calculus Techniques of Integration Today's Homework Log into WebWorK Quiz The Fundamental Theorem of Calculus Quiz Techniques of Integration Quiz Examples The Scholastic Aptitude Test (SAT) is rescaled so that the scores of n people, ranging from 0 to 1600, fit a distribution in the shape of the following function: f(x) = sin(πx/1600) (nπ/3200). What is the probability that a random person will score between 1200 and 1250? Find the derivative of a product of a function and an integral. Find the derivative of a product of a function and an integral. Find the integral from 0 to π/4 of tan(x). Use integration by parts to find an expression for the integral from 0 to π/4 of sin(x)5. taking u = (sin(x))4 and dv = sin(x) dx. Find the integral of x2ex. Videos Use the fundamental theorem of calculus for definite integrals (1) Use the fundamental theorem of calculus for definite integrals (2) Find the area under y = x4 between x = 1 and x = 5 Find the integral from –1 to 1 of x3 Doing the chain rule, backwards Integrate ex/(1 + e2x) Integrate (sin(x))4 ·(cos(x))3 Integrate (x + 2)/√(x2 + 4x + π) Integrate x27 + 3sin(x) Integrate Ax2 + Bx + C

Lecture 22 | Index | Lecture 24