Resources Math 3 Course Home Page Math 3 Course Syllabus Practice Exams Textbook Home Page Post a Comment

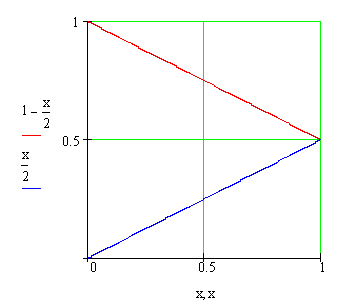
Contents In this lecture we discuss the Trapezoid Rule, a numerical technique for evaluating (approximately) a definite integral. We also discuss a formula for finding the area between two curves. Quick Question What is the area between the two curves f(x) = 1 − x/2 (in red) and g(x) = x/2 (in blue)? Answer Outline Outlines for The Trapezoid Rule Area Between Curves Textbook The Trapezoid Rule and Simpson's Rule Area Between Curves Today's Homework Log into WebWorK Quiz The Trapezoid Rule Quiz Area Between Curves Quiz Examples Approximate the integral from 0 to 2 of √x with 4 trapezoids. Sketch a figure showing the curve and the trapezoids involved. Compare your answer with the answer you find using integration formulas. Compare the 5-subinterval trapezoid approximation of the integral from 0 to 9 of x3 + 3 with the exact value of the integral. How great is the difference between them? How accurate is the Trapezoid Rule for approximating integrals? Find the area of the region bounded by y2 = 2x and x – y = 4. Sketch the region. Find the area between y = x2/4 and y = x/2 + 2. Sketch the region. Consider the region between the circles x2 + y2 = a2 and x2 + y2 = b2 in the first quadrant. Divide this region into two pieces with the curve defined by x2/a2 + y2/b2 = 1 in the first quadrant. Find the ratio of the two regions created and sketch them. Applets Numerical Integration Videos Estimate the integral of x2 dx from 0 to 6 using the Trapezoid Rule with 6 trapezoids. Find the area between x2 and √x Find the area between y = x2 and y = 2 – x2 Find the area between the ellipse x2/9 + y2 = 1 and the circle x2 + y2 = 1

Lecture 23 | Index | Lecture 25