


Next: About this document ...
Math 23
Exam 1 Practice Problems
- 1.
- Solve the following initial value problem:
- 2.
- Consider the general first order linear differential equation
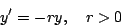 |
(1) |
- (a)
- State the general solution to the equation
- (b)
- What can you say about the behavior of solutions as
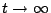 ?
?
- 3.
- Consider the DE
- (a)
- Find a solution to Equation (
![[*]](/usr/lib/latex2html/icons.gif/cross_ref_motif.gif) ) which is a linear function.
) which is a linear function.
- (b)
- Find the general solution to the homogeneous equation.
- 4.
- Find two linearly independent solutions to the
differential equation
- 5.
- Solve the initial value problem
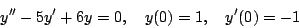 |
(4) |
- 6.
- Find the limit of the sequence
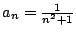 ,
and prove that it exists using the definition of convergence.
,
and prove that it exists using the definition of convergence.
- 7.
- (a)
- Compute the Taylor series for
f(x) = ex2 about x = 0.
- (b)
- Compute the Taylor series for
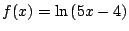 about x = 1, and find
the radius of convergence.
about x = 1, and find
the radius of convergence.
- 8.
- (a)
- Find the Taylor series for
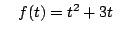 about t=0.
about t=0.
- (b)
- Prove that if
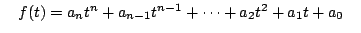 is any polynomial, then the Taylor series for f about t=0 is f
itself.
is any polynomial, then the Taylor series for f about t=0 is f
itself.
- 9.
- State whether each of the following series converges or diverges. You
do not need to give an explanation. You need not actually find the sum.
- (a)
-
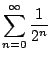
- (b)
-
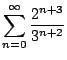
- (c)
-
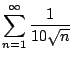
- (d)
-
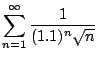
- (e)
-
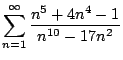
- (f)
-
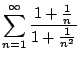
- (g)
-
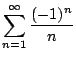
- (h)
-
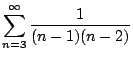
- (i)
-
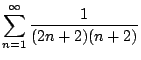
- 10.
- At time t=0, a 1000 gallon tank is full of a 5% potassium
chloride (KCl) solution. The tank is to be rinsed by having clean
water flow into the tank at the rate of 15 gallons/min, and the
well-mixed solution flowing out at the same rate.
- (a)
- Write down the differential equation governing the
concentration of KCl in the tank at time t.
- (b)
- How long will it take the concentration of KCl in the tank to
reach .1%?
- (c)
- What is the minimum input/output flow rate of fresh water that
will allow the tank mixture to drop from 5% to .1% in one hour?
- 11.
- An object of mass m falling near the surface of the earth is retarded by air
resistance proprotional to its speed. Let v(t) denote the object's velocity at time
t, and let g denote the (constant) acceleration due to gravity.
- (a)
- Verify that this DE has exactly one equilibrium solution. Find it, and
state
whether it is asymptotically
stable or unstable. Explain (pictures may help).
- (b)
- What is the physical meaning of the equilibrium solution you found
above? I.e.
what does it say about the speed of a falling object near the earth's surface?
- 12.
- Recall that Newton's law of cooling states that the rate of change of
the
temperature of an object is proportional to the difference between the temperature
of the object and the
temperature of the surrounding environment. Assume that, for a certain object, the
constant of proportionality is k=-0.2 (Assume that units on k are 1/min.). Now
assume that that object is at 150 degrees
when you place it into a room whose temperature is oscillating according to
the function
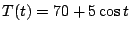 (where t represents minutes after the object was
placed
in the room).
(where t represents minutes after the object was
placed
in the room).
Find the temperature of the object at any time 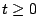 .
.
HELPFUL NOTE: for all a,
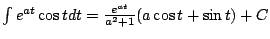



Next: About this document ...
Math 23 Winter 2000
2000-01-23
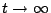 ?
?
![[*]](/usr/lib/latex2html/icons.gif/cross_ref_motif.gif) ) which is a linear function.
) which is a linear function.
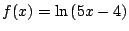 about x = 1, and find
the radius of convergence.
about x = 1, and find
the radius of convergence.
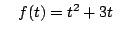 about t=0.
about t=0.
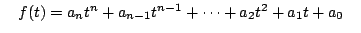 is any polynomial, then the Taylor series for f about t=0 is f
itself.
is any polynomial, then the Taylor series for f about t=0 is f
itself.
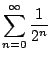
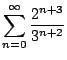
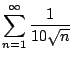
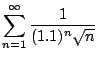
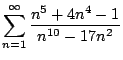
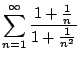
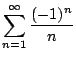
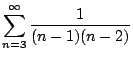
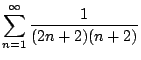
![]() .
.
![]()