


Next: Finding the nearest minimum
Up: The hunt for local
Previous: The hunt for local
Form of tension minima and resulting accuracy in 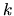
As discussed in Section 5.3.1 (also see Appendix J),
the values 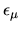 of these minima at each
of these minima at each 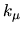 is determined
by the quality of the Helmholtz
basis set.
Around each minimum the tension is quadratic,
is determined
by the quality of the Helmholtz
basis set.
Around each minimum the tension is quadratic,
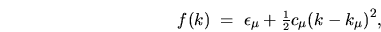 |
(5.23) |
where the curvatures 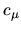 are very similar for all states
are very similar for all states 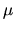 (see Fig. 5.2).
This happens because the lowest tension state of constant norm (that is, the
state
(see Fig. 5.2).
This happens because the lowest tension state of constant norm (that is, the
state 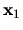 returned by (5.14)) is simply the
scaling eigenfunction
returned by (5.14)) is simply the
scaling eigenfunction 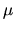 with lowest tension
(see Section 6.1.1).
The tension expansion of this function about
with lowest tension
(see Section 6.1.1).
The tension expansion of this function about 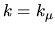 is quadratic with
is quadratic with
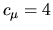 exactly, independent of
exactly, independent of 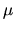 , for a modified weight function
, for a modified weight function
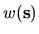 (see Appendix I).
Therefore with our choice
(see Appendix I).
Therefore with our choice
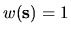 , a curvature estimate is
, a curvature estimate is
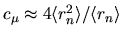 where the averages are
taken over
where the averages are
taken over
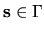 , and
, and
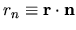 .
If either there is little scarring or the billiard is close to spherical,
then we expect this estimate to be good.
.
If either there is little scarring or the billiard is close to spherical,
then we expect this estimate to be good.
Eq.(5.23) defines a natural `error scale' for the 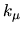 found:
a change
found:
a change 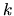 that is much less than
that is much less than
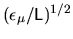 from a
tension minimum
causes only a small fractional change in tension.
Therefore I will call
from a
tension minimum
causes only a small fractional change in tension.
Therefore I will call
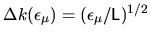 the `tension rounding error' of the
state
the `tension rounding error' of the
state 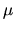 , because it defines an uncertainty in
, because it defines an uncertainty in 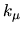 due to the
basis-dependent finite tension minima.
In practice, the errors in
due to the
basis-dependent finite tension minima.
In practice, the errors in 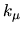 found appear to be an order of magnitude better
than
found appear to be an order of magnitude better
than
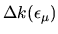 , as shwon by the lines in Fig. 6.6.
, as shwon by the lines in Fig. 6.6.



Next: Finding the nearest minimum
Up: The hunt for local
Previous: The hunt for local
Alex Barnett
2001-10-03
![]() of these minima at each
of these minima at each ![]() is determined
by the quality of the Helmholtz
basis set.
Around each minimum the tension is quadratic,
is determined
by the quality of the Helmholtz
basis set.
Around each minimum the tension is quadratic,
![]() found:
a change
found:
a change ![]() that is much less than
that is much less than
![]() from a
tension minimum
causes only a small fractional change in tension.
Therefore I will call
from a
tension minimum
causes only a small fractional change in tension.
Therefore I will call
![]() the `tension rounding error' of the
state
the `tension rounding error' of the
state ![]() , because it defines an uncertainty in
, because it defines an uncertainty in ![]() due to the
basis-dependent finite tension minima.
In practice, the errors in
due to the
basis-dependent finite tension minima.
In practice, the errors in ![]() found appear to be an order of magnitude better
than
found appear to be an order of magnitude better
than
![]() , as shwon by the lines in Fig. 6.6.
, as shwon by the lines in Fig. 6.6.