Exchange and Mentoring

Exchange

I have always enjoyed traveling and have lived in many different places and parts of the world. Traveling allows students to experience different cultures, get to know new people and broaden their worldview. To promote this enriching experience interested students in statistics and biomathematics can contact me for an exchange in one of the following places.

+++ NEWS: Due to Covid 19 it is not possible to plan exchanges at the moment +++

Stockholm, Sweden - Wenner Gren Institute - Department of Molecular Biosciences

with Martin Jastroch

Martin Jastroch studies mitochondria and cellular energy metabolisms. He wants to understand how thermogenesis evolved and how an increased understanding regarding this fundamental process can be applied to develop novel medical intervention strategies directed towards curing metabolic diseases. His groups work integrates research on whole animal metabolism with cellular and mitochondrial bioenergetics. It aims to identify molecular mechanisms and their significance for systemic energy homeostasis and metabolic disease.

Avignon, France - INRA Biostatistics and Spatial Processes

with Thomas Opitz

Thomas Opitz works in stochastic geometry and in spatial and spatiotemporal statistics with a view towards extreme values. His research includes applications to meteorological and climatic processes (precipitation, wind speeds, temperatures), spatial and spatiotemporal modeling of plant and animal species, but also analysis of extreme values and risk.

Past

At my previous workplace at Dartmouth College the following students have been participating in the exchange program:

INRA Biostatistics and Spatial Processes, Avignon: Hugo Nam, Fall 2019

British Antarctic Survey, Cambridge: Archita Harathi and Alex Stankard, Summer 2019

Wenner Gren Institute, Stockholm: Jacob Fyda and Connor Spencer, Summer 2019

MPI for Evolutionary Anthropology, Leipzig: Megan Green, Kyle Bensink and Anuraag Bukkuri, Summer 2018

Upcoming

Students should be proactive and motivated with experience in (bio)-statistics / modelling and data analysis and if possible with R. Funding should come from the college or your own resources. Interested students should feel free to contact me.



Mentoring

Since 2018 I have mentored about twenty students in a variety of activities. My area of research lies within hyperbolic and systolic geometry. Undergraduate students interested in independent study or working on a research project should feel free to email me. I am also currently working on a software project for games inspired by Linear Algebra and am always looking for students to help me develop new games. Helpers for my outreach program in geometry are equally welcome. A short summary can be found below.

Hyperbolic geometry and Riemann surfaces

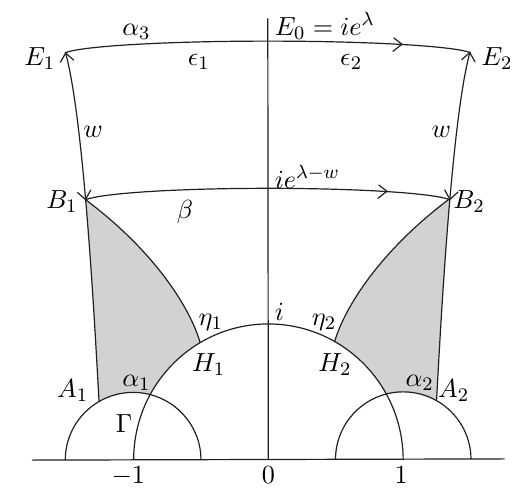
The hyperbolic plane is a space of constant negative curvature minus one, where different rules than in Euclidean space apply for geodesics, the geometry of polygons and the area of disks. A hyperbolic surface can be seen as a polygon in the hyperbolic plane with identified sides. We call such a surface a Riemann surface. Many questions about Riemann surfaces are still open or under study. Hyperbolic geometry is used in the theory of special relativity, particularly Minkowski spacetime.

Systolic geometry


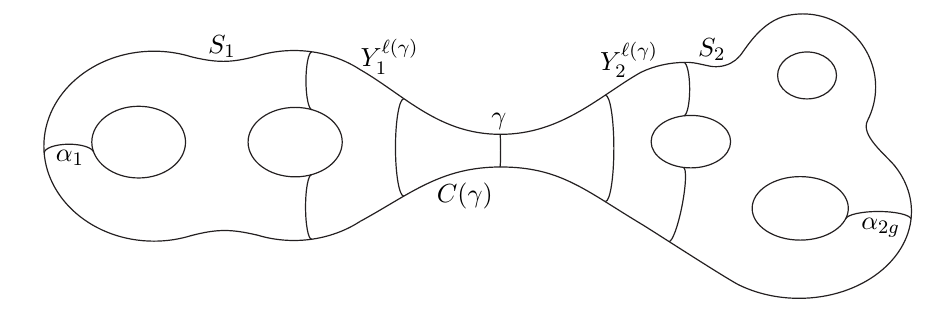 A systole of a surface is a shortest non-contractible loop on a surface. Every surface has a genus \( g \), where informally \( g \) denotes the number of holes. Surprisingly given any surface of fixed genus \( g \) and area one, the systole can not take a value larger than \(c \cdot \frac{\log(g)}{ \sqrt{g}} \), where \( c \) is a constant. A large number of families of short curves on surfaces satisfy this upper bound and example surfaces can be found among the hyperbolic Riemann surfaces.

Linear Games

see webpage.

Only four out of ten high school students feel engaged in class (Gallup, 2015) and half of the students feel bored and tired. Especially concerned by this trend is the subject math. A very recent idea to solve this problem is the gamification of math. Following this approach we develop several computer games that teach high school and college students math in a fun and open setting. Here we focus on Linear Algebra whose mastery is essential for almost all basic sciences.
The games are puzzle games which can be solved using methods from Linear Algebra. To focus on the algorithmic side instead of complicated calculations we replace the real numbers by a simpler number system which in these games is represented by pieces on a Go board. The games will be accompanied by a detailed description of the mathematics behind these games and its application.

Past

Undergraduate Research

Software Project

Outreach in Geometry

Reading Courses / Qual preparation