The Car and the Wind

Question: There is a car with a weathervane attached to its roof. (Why would anyone attach a weathervane to the roof of their car?) As the car drives north at a speed of 50 kph, the weathervane indicates that the wind is coming from due west. As the car drives north at 100 kph, the weathervane indicates that the wind is coming from the northwest. From what direction is the wind really coming? And what is the wind's speed?

Answer: First we need to introduce some notation and set up the problem. Let the vector w represent the true speed $w$ and direction $\theta$ of the wind, i.e. this is the speed of the wind relative to the ground:

$${\bf w}_{\mbox{wind/ground}} = w \cos\theta {\bf i} + w \sin\theta {\bf j}.$$ (1)

Where do the $\cos\theta$ and $\sin\theta$ come from? They come from the following picture which some (all?) of you may have seen before:

I can use the angle $\theta$ to indicate which way the wind is blowing. Therefore, to find the speed and direction of the wind, we need to find $w$ and $\theta$.

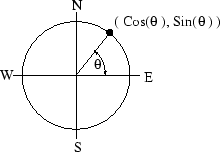
What do we know? We are given two situations. The first situation occurs when the car is travelling due north at 50 kph. Using the way I've labeled the axes in the above picture, this means that the speed of the car relative to the ground is

$${\bf v}_{\mbox{car/ground}} = 50{\bf j}.$$

In this case, the weathervane says that the wind is coming from due west. So the speed and direction of the wind, relative to the car, is

$${\bf v}_{\mbox{wind/car}} = v_1 {\bf i}.$$

Remember, all I know is that the wind seems to be coming from the west. I don't know its speed. I denote the unknown speed $v_1$. Therefore, the speed and direction of the wind relative to the ground is

$${\bf v}_{\mbox{wind/ground}} = {\bf v}_{\mbox{wind/car}} + {\bf v}_{\mbox{car/ground}}$$

$$= v_1 {\bf i} + 50{\bf j}.$$ (2)

The second situation has to do when the car is travelling due north at 100 kph:

$${\bf v}_{\mbox{car/ground}} = 100{\bf j}.$$

In this case, the weather vane says that the wind is coming from the northwest. So the speed and direction of the wind, relative to the car, is

$${\bf v}_{\mbox{wind/car}} = v_2\cos(-\pi/4){\bf i} + v_2\sin(-\pi/4){\bf j}$$

$$= v_2\frac{\sqrt{2}}{2}{\bf i} - v_2\frac{\sqrt{2}}{2}{\bf j}$$

As in the first situation, I do not know how fast the wind appears to be coming from the northwest. All I know is that it is coming from the northwest. So let $v_2$ denote the unknown speed in this situation. Therefore, the speed and direction of the wind relative to the ground is

$${\bf v}_{\mbox{wind/ground}} = {\bf v}_{\mbox{wind/car}} + {\bf v}_{\mbox{car/ground}}$$

$$= v_2\frac{\sqrt{2}}{2}{\bf i} - v_2\frac{\sqrt{2}}{2}{\bf j} + 100{\bf j}$$

$$= v_2\frac{\sqrt{2}}{2}{\bf i} + \left(100 - v_2\frac{\sqrt{2}}{2}\right) {\bf j}$$ (3)

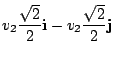I now have three different vectors representing the speed and direction of the wind relative to the ground: Equations 1, 2 and 3. All these three vectors are equal. So let me start solving for the unknown quantities $v_1$, $v_2$, $w$ and $\theta$.

Solving for $v_2$ seems easiest, because I can equate the j components in Equations 2 and 3:

$$\left(100 - v_2\frac{\sqrt{2}}{2}\right) = 50$$

Solving the above for $v_2$ yields $v_2 = 50\sqrt{2}$. And that means Equation 3 is (plugging in the value for $v_2$):

$${\bf v}_{\mbox{wind/ground}} = 50 {\bf i} + 50 {\bf j}.$$ (4)

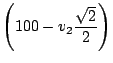Equating the ${\bf i}$ and ${\bf j}$ components of Equations 1 and 4, I get $w \cos\theta = 50$ and $w \sin\theta = 50$. Therefore

$$w \cos\theta = w \sin\theta \Rightarrow \cos\theta=\sin\theta.$$

For what values of $\theta$ is the above true? For $${\theta = \frac{\pi}{4}\mbox{ and }\frac{5 \pi}{4}.}$$ Which $\theta$ do we choose?

By studying the circle picture we started with and seeing where the wind appears to be coming from when the car drives at 50 kph and 100 kph, we can reason that the wind will be coming somewhere from the west. (Draw vectors that indicate the two directions the wind seems to be heading. As the car slows down from 100 kph to 50 kph, how are the two ``wind'' vectors you drew changing?) So that means the wind is coming from the southwest: $${\theta = \frac{\pi}{4}}$$.

And now I can finally solve for $w$, the speed of the wind. I'll do this by equating the ${\bf i}$ components of Equations 1 and 3:

$$v_2 \frac{\sqrt{2}}{2} = w \cos\theta$$

$$50\sqrt{2}\left(\frac{\sqrt{2}}{2}\right) = w \cos\left(\frac{\pi}{4}\right)$$

$$50 = w \frac{\sqrt{2}}{2}$$

$$50 \sqrt{2} = w.$$

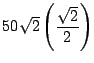Therefore, the wind is coming from the southwest at a speed of $50\sqrt{2}$ kph (and I never had to solve for $v_1$). And as they say, the answer is blowing in the wind.

Note: There are other ways of solving this problem. This is just one of them.