Resources Math 3 Course Home Page Math 3 Course Syllabus Practice Exams Textbook Home Page Post a Comment

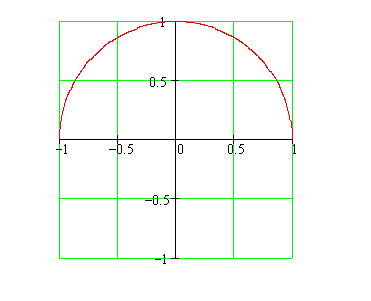
Contents In this lecture we learn that integrals can be used to compute volumes as well as areas. We apply the Method of Accumulations to develop a formula for the volume of a solid generated by revolving a plane region about the x-axis. Quick Question Rotate the following semicircular region about the x-axis. What figure results and what is its volume? Answer Textbook Volumes of Solids of Revolution Today's Homework Log into WebWorK Quiz Volumes of Solids of Revolution Quiz Examples Find the volume of the solid generated by rotating the region R bounded by the y axis, the line y = a, and the curve y = √x around the x axis. Find the volume of the solid generated by rotating the region bounded by y = x, y = 3 – x, and x = 4 around the line x = 5. Find the volume of the torus of radius a with inside radius b. Videos Find the volume of the cone created by rotating y = 3x around the x-axis between x = 0 and x = 1 Find the volume of the solid created by rotating y = cos x around the x-axis between x = 0 and x = π/2

Lecture 29 | Index