Resources Math 3 Course Home Page Math 3 Course Syllabus Practice Exams Textbook Home Page Post a Comment

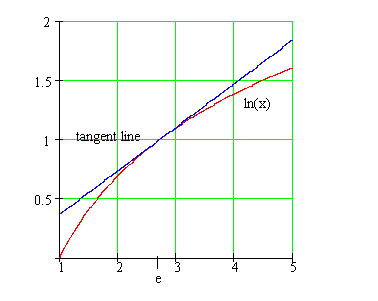
Contents In this lecture we look at two applications of the derivative: finding the zeroes of a function, and approximating the value of a function with a line. The former application leads to a numerical procedure called "Newton's Method" which, for example, is a popular technique used by calculators to find square roots. Quick Question What is the equation of the line tangent to the graph of ln(x) at x = e? Answer Textbook Newton's Method Linear Approximations Today's Homework Log into WebWorK Quiz Newton's Method Quiz Linear Approximations Quiz Examples Consider the equation x1/3 = 0 and say you intend to solve it using Newton's method. If the initial value chosen is not 0, what will happen when you apply Newton's method? Using Newton's Method, find the equation of a line tangent to the curve y = sin(x) that passes through the origin. Give the answer to 6 decimal places. Use Newton's Method to approximate to 6 decimal places the solution to the equation tan(x/4) = 1. When solving problems in geometric optics, engineers and physicists often use the simplifying assumption that, for small angles θ, sin(θ) is approximately equal to θ. Find a linear approximation for sin(x) that shows why this is a reasonable assumption. A pizza restaurant sells an average of 80 pizzas per day at its usual price of $12.95. It experiments with sales and coupons for dollars off the usual price, and finds that the number of pizzas sold when the price decreases by 2 dollars is 135. It estimates that the number of pizzas sold when the price goes down by x dollars is modeled by the function 50 ln(x + 1) + 80. Use linear approximation to find the change in the number of pizzas sold when the price drops from $10.95 to $9.95. Find the linear approximation of the function f(x) = √(1 − x) about a = 0. Use it to approximate the square root of 0.9. Applets Newton's Method Best Linear Approximation Videos Newtons method Newton's method might go wrong Newton's method bites the dust Find the equation for the tangent line of 4x2 + 10x + 5 at the point (2,1) using power rule to find formula for derivative cos(x) at π/3

Lecture 13 | Index | Lecture 15