Resources Math 3 Course Home Page Math 3 Course Syllabus Practice Exams Textbook Home Page Post a Comment

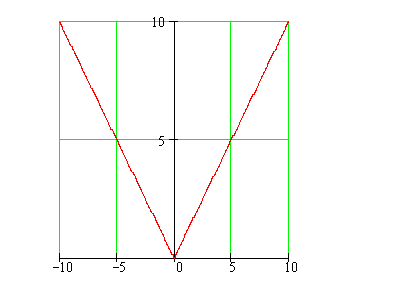
Contents In this lecture we define the concept of continuity in terms of limits. We also study the notion of the limit of tangent lines at a point, and the limit of their corresponding slopes at the point. Quick Question This is a graph of what function? Answer Outline Outlines for Continuity Tangent Lines and their Slopes Textbook Continuity Tangent Lines and their Slopes Today's Homework Log into WebWorK Quiz Continuity Quiz Tangent Lines and their Slopes Quiz Examples Find the limit of |x| as x approaches 0 from the left and from the right. Is |x| continuous at 0? Consider function f(x) that returns the biggest integer smaller than or equal to x. What can you say about the continuity of f(x)? A hiker sets out at dawn to walk over a mountain and down the other side to a lake, a distance of x kilometers, and he reaches his destination exactly 12 hours later. He camps, then leaves at the same time the next morning and travels the same trail back, arriving at his starting place 12 hours later. Use the Intermediate Value Theorem to show that at some specific time, he was at the same place on his hike on both days. Can you find a tangent line to f(x) = |x| at x = 0? A practice ski jump hill follows the shape of a given curve. Come up with a formula for the angle the skier's skis make with the horizontal, and find how far from the top of the jump he is when this angle is the greatest. A potted cactus is thrown upward with a velocity of 40 feet per second. Its height in feet at time t is given by the formula h(t) = 40t – 16t2. Find its velocity 2 seconds after it is released. Applets Continuity of Functions Secant and Tangent Lines Videos Left and right continuous defined Define slope of tangent line as limit of slopes of secant lines Find slope of tangent line to y = x2 at (1,1) Find slope of tangent line to y = √x at x = 4 Find the equation for the tangent line of 4x2 + 10x + 5 at the point (2,1) using the limit definition of the derivative Describe continuity of: f(x) = 3x for x < 1 f(x) = 4x for x ≥ 1 f(x) = 2x for x < 0, f(x) = x3 for x ≥ 0

Lecture 7 | Index | Lecture 9