Resources Math 3 Course Home Page Math 3 Course Syllabus Practice Exams Textbook Home Page Post a Comment

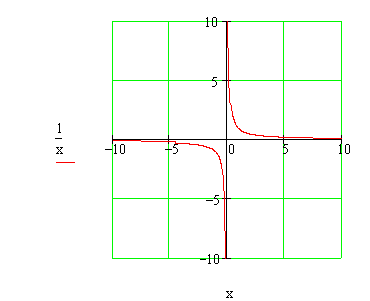
Contents In this lecture we discuss the concept of the limit of a function at a point, and of the limit of a function at plus infinity or minus infinity. Quick Question If we define f(x) = 1/x, is there any value of x for which f(x) = 0? Answer Outline Outlines for The Legacy of Galileo, Newton, and Leibniz Limits of Functions Limits at Infinity Textbook The Legacy of Galileo, Newton, and Leibniz Limits of Functions Limits at Infinity Today's Homework Log into WebWorK Quiz The Legacy of Galileo, Newton, and Leibniz Quiz Limits of Functions Quiz Limits at Infinity Quiz Examples Two taxicab drivers decide to race their cabs. The first driver has a 30-second head start, and accelerates at 1 meter per second per second. The second driver accelerates at 2 meters per second per second. How many seconds will it take for the second driver to catch the first? The distance an object falls in t seconds is given by a formula involving g, the force of gravity. If a penny is dropped from the top of the Empire State Building (350 meters tall), what is its average velocity? What is its average velocity on the [340 meters, 350 meters], that is, during its final 10 meters before it hits the ground? The gravitational acceleration on Mars is about 3.7 meters per second per second. If a Martian juggler were to throw a ball straight up at a rate of 25 meters per second, how high would the ball go? How long would it take until it came down again? Use the formulas v(t) = v0 − at for the velocity and d(t) = v0t − (1/2) at2 for the height of the ball. Find the limit of a composition of functions Find the limit of a quotient Find conditions on two variables so that two limits are equal Find horizontal and vertical asymptotes of a rational function Allyson carries an 80 degree cup of coffee into a room which has been heated to 20 degrees. According to Newton's Law of Cooling, the temperature of the coffee at time t is given by a formula. Find the temperature the coffee will reach if it is left in the room indefinitely. Find the size of a population Applets Limits of Functions Videos You hike 2 miles in 35 minutes, what is your average velocity? You hike 2 miles in 35 minutes then 4 miles in 60 minutes, what is your average velocity? You hike 2 miles in 35 minutes then 4 miles in 60 minutes then .5 miles in 6 minutes, what is your average velocity? during which segment was your average velocity the greatest? Left- and right-handed limits of a function may be different or the same Sandwich Theorem shows the limit as x approaches 0 of sin(x)/x = 1 With G(x) a piecewise defined, bumpy function: limit as x approaches 1 from the right of G(x) = 0 limit as x approaches 3 from the left of G(x) = 0 limit as x approaches 3 of G(x) = 0; limit as x approaches 1 of G(x) is undefined Evaluate these limits: f(x) = 1/(x2 – 16) limit as x approaches 7 from the right of (3x)/(x2 – 8x + 7) limit as x approaches 7 from the left of (x – 7)/(x2 – 8x + 7) limit as x approaches ∞ of x ·sin(x) limit as x approaches ∞ of sin(x)/x

Lecture 6 | Index | Lecture 8