Chapter 3.1
Ordinary Homogeneous Second Order Linear Differential Equations With Constant Coefficients

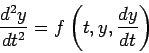
In general, a second order ordinary differential equation looks like

$$\frac{d^2y}{dt^2} = f \left( t, y, \frac{dy}{dt} \right)$$

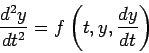
But they are too hard to solve.

We say that a second order D.E. is linear if we can write the right-hand side in the form

$$f \left( t, y, \frac{dy}{dt} \right) = g(t) - p(t)\frac{dy}{dt} - q(t)y$$

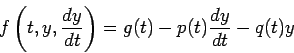
to obtain

y'' + p(t)y' + q(t)y = g(t)

for some functions p, q, and g of t.

If we cannot do this, we say the D.E. is nonlinear.

Examples:

Linear

$$3y'' - \pi y' + \sqrt{2}y = t$$

$$y'' + e^ty' - \cos{t}y = \sin{t}\ln{t}$$

Nonlinear

y y'' = 1

y'' + y' + y² = 0

A second order initial value problem consists of the differential equation

$$\frac{d^2y}{dt^2} = f \left( t, y, \frac{dy}{dt} \right)$$

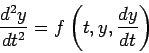
together with two initial conditions:

$$y(t_0) = y_0 \hspace{1in} y'(t_0) = y_1.$$

A second order linear D.E.

y'' + p(t)y' + q(t)y = g(t)

is called homogeneous if $g(t) \equiv 0$.

Otherwise, it is nonhomogeneous.

The Principle of Superposition

If y₁(t) and y₂(t) are solutions to the homogeneous equation

y'' + p(t)y' + q(t)y = 0,

then y(t) = c₁ y₁(t) + c₂ y₂(t) is also a solution. We say that y(t) is a linear combination of the solutions y₁(t) and y₂(t).