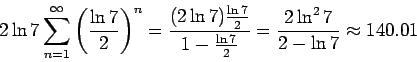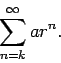
_n=k^

Geometric Series
Examples

Geometrc series are series of the form

$$\sum_{n=k}^{\infty}ar^n.$$

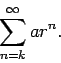
Geometric series converge for -1 < r < 1, and diverge otherwise. Their sum is given by the formula

$$\sum_{n=k}^{\infty}ar^n = \frac{ar^k}{1-r}.$$

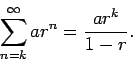
This is precisely the value of the first term (ar^k) divide by 1-r. When the sum starts at 0, this sum has a particularly simple form:

$$\sum_{n = 0}^{\infty} ar^n = \frac{a}{1-r}.$$

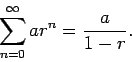
Let's try some examples.

1. Determine if the series $\sum_{n=1}^{\infty} \frac{(\ln{7})^{n+1}}{2^{n-1}}$ converges, and if so, find its sum.

Since this page deals with geometric series, you probably aren't surprised that this is in fact, a geometric series. However, it doesn't quite look like one. Our first order of business, then, should be to figure out what a and r are for this particular series.

[Note: In general, when you see a constant raised to the nth power (or some variant thereof) in both the numerator and denominator, you should think geometric series]

First, we alter the series so that the exponents in the numerator and denominator agree.

$$\begin{eqnarray*} \sum_{n = 1}^{\infty} \frac{(\ln{7})^{n+1}}{2^{n-1}} & = & \fr... ... 2\ln{7} \sum_{n = 1}^{\infty} \left( \frac{\ln{7}}{2} \right)^n \end{eqnarray*}$$

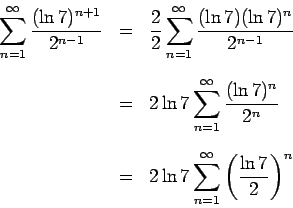
Ahhh...that looks better! From this last formula, we can observe that $a = 2\ln{7}$, and $r = \frac{\ln{7}}{2}.$ So we just need to compute r to see if the series converges. In fact is does, as $r \approx .973 < 1.$

Hence, we can also compute the sum of the series:

$$2\ln{7} \sum_{n = 1}^{\infty} \left( \frac{\ln{7}}{2} \right)... ...- \frac{\ln{7}}{2}} = \frac{2\ln^2{7}}{2-\ln{7}} \approx 140.01$$