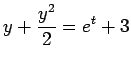
- (a)
- y(t) = C e-rt
- (b)
- As
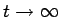 ,
,
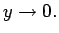
- (a)
-
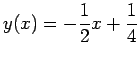 [Note: no arbitrary constant!]
[Note: no arbitrary constant!]
- (b)
- Solving y'' - y' - 2y = 0 yields y(x) = c1e2x + c2e-x.
To prove this, when given an
![\begin{eqnarray*}
& &\vert a_n\vert < \epsilon\\ [.1in]
\Longrightarrow & \quad ...
...in]
\Longrightarrow & \quad & n > \sqrt{\frac{1}{\epsilon} - 1}.
\end{eqnarray*}](img10.gif)
So, if we define M as
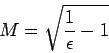
then the preceding steps, when followed backwards, will show that if
n > M, we are guaranteed that
![]() .
.
- (a)
-
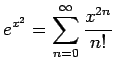
- (b)
-
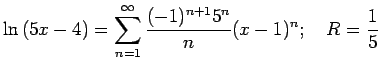
[Note: it's a good idea to double check that the summation you write down generates the same terms that you computed for the Taylor series. Sometimes it takes a little fiddling to get the factorials, exponents and negative signs to line up. Don't forget that we define 0!=1.]
- (a)
- The Taylor Series is, of course, f(t) = t2 + 3t.
- (b)
- Let's first compute the various derivatives of f(t) evaluate them at
0.
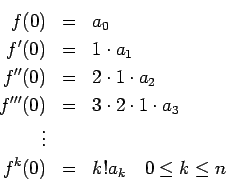
Now, when we form the Taylor polynomial coefficients we get
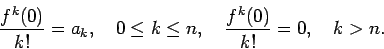
Since ak = 0 for k > n (because the (n+1)st and higher derivatives of an nth degree polynomial are zero), we get a finite sum for our Taylor series, and as we just computed, the non-zero coefficients are equal to the coefficients of f(t), hence
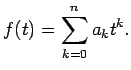
- (a)
-
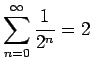
- (b)
-
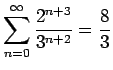
- (c)
-
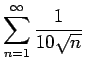 diverges
diverges
- (d)
-
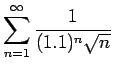 converges
converges
- (e)
-
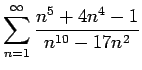 converges
converges
- (f)
-
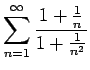 diverges
diverges
- (g)
-
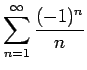 converges
converges
- (h)
-
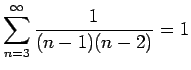
- (i)
-
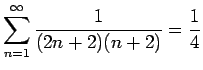
- (a)
-
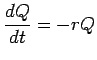
- (b)
- You should obtain
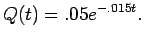 The time for the
tank to reach a concentration of .1% is 261 minutes.
The time for the
tank to reach a concentration of .1% is 261 minutes.
- (c)
- r = 65.2 gal/min.
- (a)
- Let
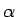 denote the coefficient of air resistance. Then the D.E. is
denote the coefficient of air resistance. Then the D.E. is
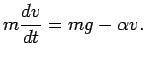 Setting
Setting
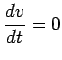 gives
the single critical point
gives
the single critical point
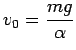 (the terminal velocity). By
plotting
(the terminal velocity). By
plotting
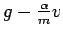 and drawing the left and right pointing arrows, you can
determine that the critical point is asymptotically stable (which should check
with our intuition).
and drawing the left and right pointing arrows, you can
determine that the critical point is asymptotically stable (which should check
with our intuition).
- (b)
- An object will accelerate until it reaches some terminal velocity, after which it will fall at a constant speed.
This was a fairly challenging problem, so give yourself a pat on the back if you were able to work it out...