Math 23 - Final Exam Practice Problems

1.

For each statement below, state whether it is true or false and give a very brief justification.

(a)

The Taylor series for 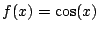$f(x)=\cos(x)$ about x=0 is $1 - \frac{1}{2!}x^2 + \frac{1}{4!}x^4 - \frac{1}{6!}x^6 + \cdots$.

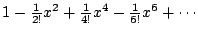(b)

The series 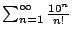$\sum_{n=1}^\infty \frac{10^n}{n!}$ converges.

(c)

2 is an eigenvalue of the matrix 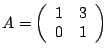$A = \left(\begin{array}{cc} 1 & 3\\ 0 & 1 \end{array}\right)$.

(d)

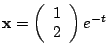${\bf x} = \left(\begin{array}{c} 1\\ 2 \end{array}\right)e^{-t}$ is a solution to the system ${\bf x}' = \left(\begin{array}{cc} 3 & -2\\ 2 & -2 \end{array}\right) {\bf x}$.

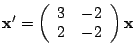(e)

If y₁ and y₂ are any two solutions to a linear homogeneous DE on an open interval I, then the Wronskian W(y₁,y₂) is either always zero or never zero on I.

(f)

If f and g are differentiable functions such that f(x) = 2g(x), then the Wronskian W(f,g) is zero.

2.

Find the general solution of the DE:

y'' - 4y' + 3y = e^2x.

3.

Find the general solution of the DE:

$$y'' - 2y' + y = \frac{e^t}{t} \qquad t > 0.$$

4.

Solve the initial value problem:

$$\left\{\begin{array}{l} y'+y=te^{-t} + 1\\ y(0)=0 \end{array}\right.$$

5.

Find the general solution of the DE:

y''-2y'+2y = 0.

6.

Define a function f by

• $f(x) = \left\{\begin{array}{cl} 0 & \qquad -1 \leq x \leq 0\\ x & \qquad 0 < x \leq 1\\ \end{array}\right.$
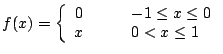
• f(x) = f(x+2) for all real numbers x.

Compute the Fourier series for f.

7.

Suppose a mass of m kg is attached to a spring with spring constant k.

(a)

Assume no air resistance and assume there is no external force acting on the system. Suppose you pull the mass down u₀ meters from its equilibrium position and then release it. Find a function u that describes the position of the mass at any time $t \geq 0$.

(b)

Assume no air resistance, but assume now that there is an external force F_e(t) acting on the mass according to the function 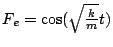$F_e = \cos(\sqrt{\frac{k}{m}}t)$. Suppose the mass starts from its equilibrium position with no initial velocity. Find a function u that describes the position of the mass at any time $t \geq 0$.

8.

Suppose a metal rod 10 cm long is constructed from a material with coefficient $\alpha^2 = 1$. Assume that the rod is initially at a uniform temperature of 50 degrees C (i.e. the temperature is 50 at every point in the rod). At time t=0, the ends of the rod are plunged into buckets of ice. This instantaneously lowers the temperature at each end to 0 degrees C, where it will remain forevermore.

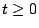Find a function u(x,t) which describes the temperature at position x in the rod at time t.

9.

Suppose a metal rod 50 cm long is constructed from a material with coefficient $\alpha^2 = .5$. Suppose the temperature distribution at time t = 0 is given by the function f(x) where

$$f(x) = \left\{\begin{array}{cl} \frac{5}{2}x + 100 & \qquad 0... ...q 20\\ -3x + 210 & \qquad 20 < x \leq 50\\ \end{array}\right.$$

The left end of the rod (x = 0) is held at a constant temperature of $100^{\circ}$F, while the right end (x = 50) is held at a constant temperature of $60^{\circ}$ F.

(a)

Find a function u(x,t) which describes the temperature at position x in the rod at time t.

(b)

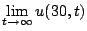Find $${\lim_{t \to \infty}{u(30,t)}}$$.

10.

Suppose f and g are linearly independent functions. Prove using the definition of linear independence that f+g and f-2g are also linearly independent.

11.

Suppose that f, g, and h are linearly dependent. Is it necessarily true that the functions f and g are linearly dependent? Justify your answer.