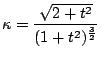Mid-term Examination, Multivariable Calculus
Math 13, Winter 1998
Date: Thursday, 11 February; 19:00 - 20:20
Instructions:
- Complete all 4 questions. You may answer the questions in any
order.
- Explain all your answers. Hand in all your working notes.
- You have 80 minutes to complete the exam.
- 1.
- (a)
- (20 points) Let
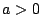 be a positive number. Find the maximum of
be a positive number. Find the maximum of
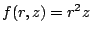 subject to the constraint that
subject to the constraint that
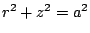 .
.
- (b)
- (5 points) What is the maximum possible volume of a cylinder
contained inside a sphere of radius
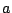 ?
?
- 2.
- (a)
- (5 points) Draw the region
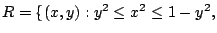 and
and 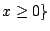 in the
in the 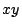 -plane.
-plane.
- (b)
- (20 points) Use polar coordinates to find the volume of the
solid region lying above
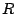 and below the surface
and below the surface
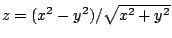 . (20 points)
. (20 points)
- 3.
- An ant is walking on a thin metal plate that occupies the region
The temperature of the plate at the point
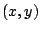 is
is
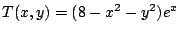 .
.
- (a)
- (10 points) Suppose the ant is at the origin. In which direction
should the ant move, so that its temperature decreases as quickly as possible?
- (b)
- (15 points) Where on the plate is the temperature the highest? What is the
maximum temperature of any point on the plate? Justify your answer.
- 4.
- A particle is travelling so that its position in
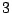 -space at
time
-space at
time 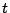 is given by
is given by
- (a)
- (10 points) Find the velocity, acceleration, and speed of the
particle at time
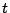 .
.
- (b)
- (10 points) Find the tangential component of acceleration of the
particle at time
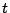 .
.
- (c)
- (5 points) Find the length of the acceleration vector at time
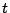 . Use this to show that the curvature of the particle's trajectory at
time
. Use this to show that the curvature of the particle's trajectory at
time 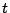 is
is
Math 13 Winter 1999
1999-03-03
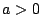 be a positive number. Find the maximum of
be a positive number. Find the maximum of
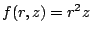 subject to the constraint that
subject to the constraint that
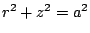 .
.
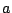 ?
?
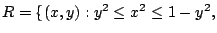 and
and 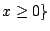 in the
in the 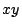 -plane.
-plane.
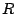 and below the surface
and below the surface
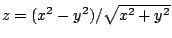 . (20 points)
. (20 points)
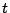 .
.
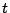 .
.
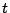 . Use this to show that the curvature of the particle's trajectory at
time
. Use this to show that the curvature of the particle's trajectory at
time 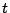 is
is