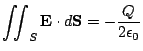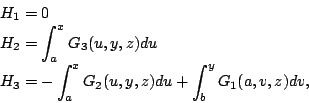- 1.
- Stewart, Section 14.8, Exercises 1, 2, 10, 19.
- 2.
- Show by direct calculation that the conclusion of Stokes
Theorem does not hold for
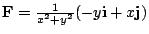 .
.
- 3.
- Let
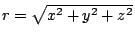 ,
,
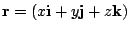
- (a)
- Find the gradient of
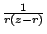 . Find the curl of
. Find the curl of
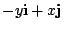 .
.
- (b)
- Show that
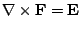 , everywhere except on the
non-negative part of the
, everywhere except on the
non-negative part of the 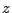 -axis, where
and
-axis, where
and
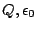 are strictly positive constants.
are strictly positive constants.
- (c)
- Let
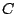 be the curve
be the curve
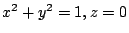 oriented in the
anti-clockwise direction when viewed from above. Use Stokes theorem
to show that if
oriented in the
anti-clockwise direction when viewed from above. Use Stokes theorem
to show that if 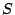 is any oriented surface with oriented boundary
is any oriented surface with oriented boundary 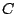 , and
, and
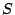 does not intersect the non-negative part of the
does not intersect the non-negative part of the 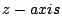 , then
, then
- 4.
- (Optional) Suppose
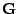 is a vector field with
is a vector field with
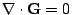 , everywhere in
, everywhere in 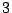 -space. Define
-space. Define
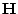 in terms of
in terms of
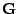 by
where
by
where 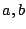 are arbitrary constants. Show by direct calculation that
are arbitrary constants. Show by direct calculation that
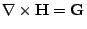 everywhere in
everywhere in 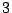 -space.
-space.
Math 13 Winter 1999
1999-03-03
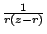 . Find the curl of
. Find the curl of
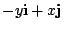 .
.
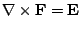 , everywhere except on the
non-negative part of the
, everywhere except on the
non-negative part of the 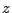 -axis, where
and
-axis, where
and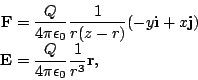
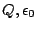 are strictly positive constants.
are strictly positive constants.
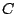 be the curve
be the curve
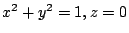 oriented in the
anti-clockwise direction when viewed from above. Use Stokes theorem
to show that if
oriented in the
anti-clockwise direction when viewed from above. Use Stokes theorem
to show that if 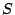 is any oriented surface with oriented boundary
is any oriented surface with oriented boundary 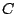 , and
, and
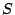 does not intersect the non-negative part of the
does not intersect the non-negative part of the 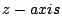 , then
, then