For calculating the rate of energy absorption
due to time-dependent deformation of the
confining potential, in this chapter I introduce an improved version
of the wall formula.
The formulation takes into account
the `special' class of deformations that cause no heating
in the zero-frequency limit, which was identified in the previous
chapter.
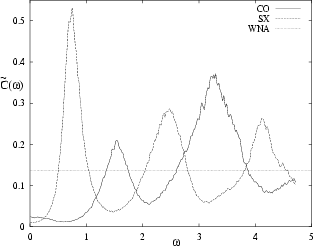
Recall that since calculation of the exact kernel (3.5) is
very complicated, we are interested in an approximate prediction for
![]() , and for the noise intensity
, and for the noise intensity
![]() in particular.
From this follows the friction coefficient
in particular.
From this follows the friction coefficient ![]() , according to
the recipe in Section 2.1.5.
, according to
the recipe in Section 2.1.5.
The simplest estimate for
![]() is
the white noise approximation (WNA) introduced in the previous chapter,
and it leads
(for a 3D cavity) to the well known `wall formula' [29]
is
the white noise approximation (WNA) introduced in the previous chapter,
and it leads
(for a 3D cavity) to the well known `wall formula' [29]
The main purpose is to introduce an improved version of the
wall formula, in the form of an improved estimate for
![]() , which I
will call the `IFIF' (Section 4.3).
This improvement involves
projecting out the special components of a general deformation,
and only then to estimate
, which I
will call the `IFIF' (Section 4.3).
This improvement involves
projecting out the special components of a general deformation,
and only then to estimate
![]() using the WNA.
This will give an estimate which handles many forms of
using the WNA.
This will give an estimate which handles many forms of
![]() better
than the plain WNA, as I demonstrate numerically.
better
than the plain WNA, as I demonstrate numerically.
 |