Some sample theorems

$\begin{lemma} Let's put here exactly what we need to prove the next theorem. \end{lemma}$

$\begin{thm} Let $f$\ be a nonzero element of $S_{k/2}(4N,\psi)$. Then there exi... ...umber of square-free positive integers $t$ such that $\Sh_t(f) \ne 0$. \end{thm}$

The proof which is below is correct, but unmotivated. Perhaps we can find an alternate proof which provides more insight

Proof. If $\Sh_t(f) = 0$ for all but a finite number of square-free positive integers

, then by lemma:squareclasses the Fourier coefficients of

are supported on only a finite number of square classes. By Theorem 3 of [3] the weight of

must be

and at weight

must be in the span of the theta series $h_\psi$ , contrary to assumption. $\qedsymbol$

$\begin{defn} A horse is a horse of course, of course, but noone can talk to a horse of course \dots. \end{defn}$

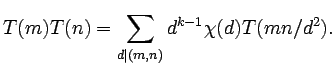$\displaystyle T(m) T(n) = \sum_{d \mid (m,n)} d^{k-1}\chi(d) T(mn/d^2).$

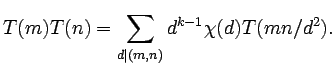(1)

Here is the same expression, but inline and not displayed. Notice it is set smaller and the summation indeices are placed differently: $T(m) T(n) = \sum_{d \mid (m,n)} d^{k-1}\chi(d) T(mn/d^2).$ Note I need to use $ to surround my formula when in an inline mode.

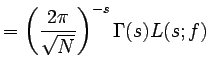$\displaystyle \Lambda_N(s;f)$	$\displaystyle = \left(\frac{2\pi}{\sqrt N}\right)^{-s} \Gamma(s) L(s;f)$
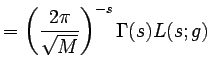$\displaystyle \Lambda_M(s;g)$	$\displaystyle = \left(\frac{2\pi}{\sqrt M}\right)^{-s} \Gamma(s) L(s;g)$

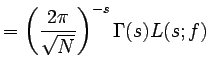$\displaystyle \Lambda_N(s;f)$	$\displaystyle = \left(\frac{2\pi}{\sqrt N}\right)^{-s} \Gamma(s) L(s;f)$	(2)
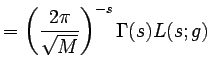$\displaystyle \Lambda_M(s;g)$	$\displaystyle = \left(\frac{2\pi}{\sqrt M}\right)^{-s} \Gamma(s) L(s;g)$	(3)

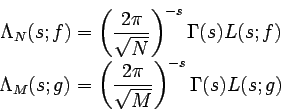$\begin{displaymath}\begin{split}\Lambda_N(s;f) &= \left(\frac{2\pi}{\sqrt N}\rig... ...t(\frac{2\pi}{\sqrt M}\right)^{-s} \Gamma(s) L(s;g) \end{split}\end{displaymath}$

(4)

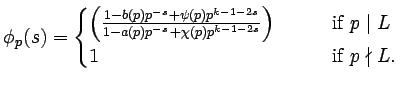$\displaystyle \phi_p(s) = \begin{cases}\left(\frac{1 - b(p) p^{-s} + \psi(p) p^... ...\right) &\qquad \text{if } p\mid L\\ 1&\qquad\text{if } p \nmid L. \end{cases}$

This should be more than enough displayed equations for the average person. Gosh, I sure hope this paper gets accepted. More remarks of little permanent consequence.

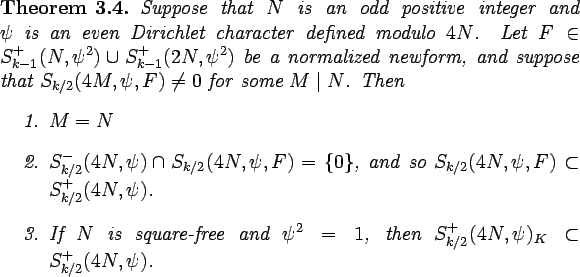
$\begin{thm}Suppose that $N$\ is an odd positive integer and $\psi$\ is an even ... ...hen $S^+_{k/2}(4N,\psi)_K \subset S^+_{k/2}(4N,\psi)$. \end{enumerate}\end{thm}$