Description and Requirements
The Book
Bibliography
Syllabus
 Introduction
Introduction The Great Pyramid
The Great Pyramid Music of the Spheres
Music of the Spheres  Number Symbolism
Number Symbolism  Polygons and Tilings
Polygons and Tilings  The Platonic Solids
The Platonic Solids  Roman Architecture
Roman Architecture  Number Symbolism in the Middle Ages
Number Symbolism in the Middle Ages  The Wheel of Fortune
The Wheel of Fortune  Celestial Themes in Art
Celestial Themes in Art  Origins of Perspective
Origins of Perspective  What Shape Frame?
What Shape Frame?  Piero della Francesca
Piero della Francesca  Leonardo
Leonardo  Façade measurement by Trigonometry
Façade measurement by Trigonometry  Early Twentieth Century Art
Early Twentieth Century Art Dynamic symmetry & The Spiral
Dynamic symmetry & The Spiral  The Geometric Art of M.C. Escher
The Geometric Art of M.C. Escher  Later Twentieth Century Geometry Art
Later Twentieth Century Geometry Art  Art and the Computer
Art and the Computer  Chaos & Fractals
Chaos & Fractals
The PLATONIC SOLIDS
"Let no one destitute of geometry enter my doors."
Plato (c. 427 - 347 B.C.E.)

American Catalgo, p. 126, #21061. Fresco, Vatican, Stanza della Signurata, the Pope's Private Library
We now move forward in time about 150 years, still staying in Greece, from Pythagoras to Plato, himself a Pythagorean.
In our last unit we studied some polygons, and I said that one of these, the triangle, was thought by Plato to be the building block of the universe. He presented that idea and others about creation, such as the universe being created to resemble a geometric progression, in one of his books, the Timaeus.
In the Timaeus, we'll see how Plato describes how triangles make up five solids, now called the Platonic Solids, and how these solids make up the four elements and heaven. We'll look at regular polyhedra in general, and see why only five are possible.
Finally we'll see how the Platonic solids were used as art motifs even before Plato, how they were used later, and how the served to tie together three Renaissance mathematicians and artists, Piero della Francesca, Luca Pacioli, and Leonardo da Vinci.
| Outline: | Plato |
| The Timaeus | |
| Music of the Spheres | |
| The Elements | |
| The Platonic Solids | |
| Polyhedra | |
| Polyhedra in Art & Architecture | |
| Summary |
Plato
 |
Slide 6-2: RAPHAEL: School of Athens. Center section |
Profile: Plato (c.427-347 B.C.E.) was born to an aristocratic family in Athens. As a young man Plato had political ambitions, but he became disillusioned by the political leadership in Athens. He eventually became a disciple of Socrates, accepting his basic philosophy and dialectical style of debate, the pursuit of truth through questions, answers, and additional questions. Plato witnessed the death of Socrates at the hands of the Athenian democracy in 399 BC. In Raphael's School of Athens we see Socrates prone, with cup nearby.
Plato's most prominent student was Aristotle, shown here with Plato in Raphael's School of Athens, Aristotle holiding his Ethics and Plato with his Timaeus.
Plato's Academy
In 387 BCE Plato founded an Academy in Athens, often described as the first university. It provided a comprehensive curriculum, including astronomy, biology, mathematics, political theory, and philosophy.
Plato's final years were spent lecturing at his Academy and writing. He died at about the age of 80 in Athens in 348 or 347.
Over the doors to his academy were the words

meaning, "Let no one destitute of geometry enter my doors."
Plato on Art and Geometry
Although Plato loved geometry, he would not have been good at teaching a course in Art & Geometry because he had a low opinion of art. He taught that, since the world is a copy or image of the real, then a work of art is a copy of a copy, at third remove from reality.
He writes in his Republic(p. 603),
"... painting [and] ... the whole art of imitation is busy about a work which is
far removed from the truth; ... and is its mistress and friend for no wholesome or
true purpose. ... [it] is the worthless mistress of a worthless friend, and the
parent of a worthless progeny."
But on geometry he wrote in his Republic (p. 527),
"[Geometry is] . . . persued for the sake of the knowledge of
what eternally exists, and not of what comes for a moment into existence,
and then perishes, ...
[it] must draw the soul towards truth and give the finishing touch
to the philosophic spirit."
The Timaeus
Plato left lots of writings. We've mentioned his Republic in our unit on number symbolism in which he gave the four cardinal virtues, but his love of geometry is especially evident in the Timaeus.
Written towards the end of Plato's life, c. 355 BCE, the Timaeus describes a conversation between Socrates, Plato's teacher, Critias, Plato's great grandfather, Hermocrates, a Sicilian statesman and soldier, and Timaeus, Pythagorean, philosopher, scientist, general, contemporary of Plato, and the inventor of the pulley. He was the first to distinguish between harmonic, arithmetic, and geometric progressions.
In this book, Timaeus does most the talking, with much homage to Pythagoras and echos of the harmony of the spheres, as he describes the geometric creation of the world.
Music of the Spheres
Plato, through Timaeus, says that the creator made the world soul out of various ingredients, and formed it into a long strip. The strip was then marked out into intervals.
| First [the creator] took one portion from the whole | (1 unit) |
| and next a portion double the first | (2 unit) |
| a third portion half again as much as the second | (3 unit) |
| the fourth portion double the second | (4 unit) |
| the fifth three times the third | (9 unit) |
| the sixth eight times the first | (8 unit) |
| and the seventh 27 tmes the first | (27 unit) |
They give the seven integers; 1, 2, 3, 4, 8, 9, 27. These contain the monad, source of all numbers, the first even and first odd, and their squares and cubes.
Plato's Lambda
 |
Slide 8-72 : Arithmetic Personified as a Woman
Lawlor, Robert. Sacred Geometry. NY: Thames & Hudson, 1982. p. 7. |
These seven numbers can be arranged as two progressions
Monad 1 Point
First even and odd 2 3 Line
Squares 4 9 Plane
Cubes 8 27 Solid
This is called Plato's Lambda, because it is shaped like the Greek letter lambda.
Divisions of the World Soul as Musical Intervals
Relating this to music, if we start at low C and lay off these intervals, we get 4 octaves plus a sixth. It doesn't yet look like a musical scale. But Plato goes on to fill in each interval with an arithmetic mean and a harmonic mean. Taking the first interval, from 1 to 2, for example,
Arithmetic mean = (1+2)/2 = 3/2
The Harmonic mean of two numbers is the reciprocal of the arithmetic mean of their reciprocals.
For 1 and 2, the reciprocals are 1 and 1/2, whose arithmetic mean is 1+ 1/2 ÷ 2 or 3/4. Thus,
Harmonic mean = 4/3
Thus we get the fourth or 4/3, and the fifth or 3/2, the same intervals found pleasing by the Pythagoreans. Further, they are made up of the first four numbers 1, 2, 3, 4 of the tetractys.
Filling in the Gaps
He took the interval between the fourth and the fifth as a full tone. It is
3/2 ÷ 4/3 = 3/2 x 3/4 = 9/8
Plato then has his creator fill up the scale with intervals of 9/8, the tone. This leaves intervals of 256/243 as remainders, equal to the half tone.
Thus Plato has constructed the scale from arithmetic calculations alone, and not by experimenting with stretched strings to find out what sounded best, as did the Pythagoreans.
Project: Repeat Plato's calculations and see if you do indeed get a musical scale.
Forming the Celestial Circles
After marking the strip into these intervals, the creator then cut it lengthwise into two strips that are placed at an angle to each other and formed into circles. These correspond to the celestial equator and the ecliptic, the start of an armillary sphere.
 |
Slide 10-121: Armillary Sphere
Turner, Gerard. Antique Scientific Instruments. Dorset: Blandford, 1980. p. 61 |
Recall our quotation from Plato's Republic, where, in the Myth of Er he wrote,
". . . Upon each of its circles stood a siren who was carried round with its movements, uttering the concords of a single scale." [Republic p. 354]
This is the origin of the expression, Music of the Spheres.
The Elements
The idea tthat all things are composed of four primal elements: earth, air, fire, and water, is attributed to Empedocles (circa 493-433 BCE), Greek philosopher, statesman, and poet. He was born in Agrigentum (now Agrigento), Sicily, and was a disciple of Pythagoras and Parmenides.
Remember the opposite forces, Yin and Yang, male and female, whose interaction created everything in the universe? Empedocles thought that active and opposing forces, love and hate, or affinity and antipathy, act upon these elements, combining and separating them into infinitely varied forms.
He believed also that no change involving the creation of new matter is possible; only changes in the combinations of the four existing elements may occur.
Empedocles died about 6 years before Plato was born.
The Universe as a Geometric Progression
Plato deduces the need for the four elements. Timaeus, 31B-32C
1. First, we must have fire, to make the world visible, and earth to make it resistant to touch. These are the two extreme elements, fire belonging to heaven and earth to earth. He writes,
. . . it is necessary that
nature should be visible and tangible ...
and nothing can be visible without fire or tangible without earth ...
2. But two cannot hold together without a third as a bond. [like glue]
. . . But it is impossible for two things to cohere without the intervention of a third ...
3. And the most perfect bond is the connued geometric proportion.
... [and] the most beautiful analogy is when in
three numbers,
the middle is to the last as the first to the middle, . . .
they become the same as to relation to each other.
4. But the primary bodies
are solids, and must be represented by solid numbers (cubes).
To connect two plane numbers (squares) one mean is enough,
but to connect two solid numbers, two means are needed.
But if the universe were to have no depth, one medium would suffice to bind all the natures it contains. But . . . the world should be a solid, and solids are never harmonized by one, but always by two mediums.
Hence the Divinity placed water and air in the middle of fire and earth, fabricating them in the same ratio to each other; so that fire might be to air as air is to water and that water is to earth.
Thus the ratio is constant between successive elements, giving a geometric progression.
The Platonic Solids
The Platonic Solids belong to the group of geometric figures called polyhedra.
A polyhedron is a solid bounded by plane polygons. The polygons are called faces; they intersect in edges, the points where three or more edges intersect are called vertices.
A regular polyhedron is one whose faces are identical regular polygons. Only five regular solids are possible
cube tetrahedron octahedron icosahedron dodecahedron
These have come to be known as the Platonic Solids
The Elements Linked to the Platonic Solids
Plato associates four of the Platonic Solid with the four elements. He writes,
We must proceed to distribute the figures [the solids] we have just described between fire, earth, water, and air. . .
Let us assign the cube to earth, for it is the most immobile of the four bodies and most retentive of shape
the least mobile of the remaining figures (icosahedron) to waterthe most mobile (tetrahedron) to fire
the intermediate (octahedron) to air
Note that earth is associated with the cube, with its six square faces. This lent support to the notion of the foursquaredness of the earth.
The Cosmos
But there are five regular polyhedra and only four elements. Plato writes,
"There still remained a fifth construction, which the god used for embroidering the constellations on the whole heaven."
Plato's statement is vague, and he gives no further explanation. Later Greek philosophers assign the dodecahedron to the ether or heaven or the cosmos.
The dodecahedron has 12 faces, and our number symbolism associates 12 with the zodiac.
This might be Plato's meaning when he writes of "embroidering the constellations" on the dodecahedron.
Note that the 12 faces of the dodecahedron are pentagons. Recall that the pentagon contains the golden ratio. Perhaps this has something to do with equating this figure with the cosmos.
Other Polyhedra
The Archimedian Solids

Slide 6-4: Archimedian Solids
Wenniger, Magnus J. Polyhedron Models for the Classroom. NCTM 1966. p. 7
Other sets of solids can be obtained from the Platonic Solids. We can get a set by cutting off the corners of the Platonic solids and get truncated polyhedra.
They are no longer regular; they are called semi -regular; all faces are regular polygons, but there is more than one polygon in a particular solid, and all vertices are identical.
These are also called the Archimedian Solids, named for Archimedes, (287-212) the Greek mathematician who lived in Syracusa on the lower right corner of Sicily.
Mini-Project: Make some Archimedian Solids.
Star Polyhedra
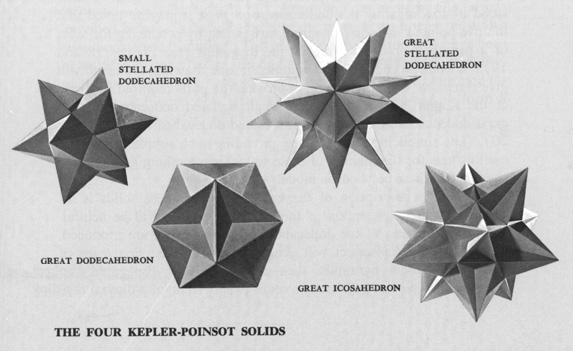
Slide 6-5: The Four Kepler-Poinsot Solids
Wenniger, Magnus J. Polyhedron Models for the Classroom. NCTM 1966. p. 11

Slide 6-6: Engraving from Harmonices Mundi, 1619.
Emmer, Michele, Ed. The Visual Mind: Art and Mathematics. Cambridge: MIT
Press, 1993. p. 218
The second obvious way to get another set of solids is to extend the faces of each to form a star, giving the so-called Star Polyhedra.
Two star polyhedra were discovered by Poinsot in 1809. The others were discovered about 200 years before that by Johannes Kepler (1571-1630), the German astronomer and natural philosopher noted for formulating the three laws of planetary motion, now known as Kepler's laws, including the law that celestial bodies have elliptical, not circular orbits.
Mini-Project: Make some star polyhedra.
Polyhedra in Art & Architecture
Polyhedra are Nothing New
Polyhedra have served as art motifs from prehistoric times right up to the present.
 |
Slide 6-7: Pyramids
Tompkins, Peter. Secrets of the Great Pyramid. NY: Harper, 1971. Cover |
The Egyptians, of course, knew of the tetrahedron, but also the octahedron, and cube. And there are icosahedral dice from the Ptolomaic dynasty in the British Museum, London.
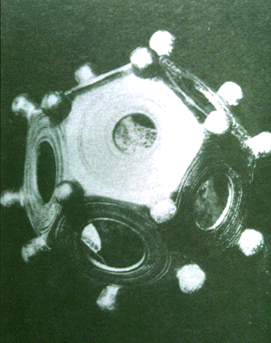 |
Slide 6-8: Etruscan Dodecahedron
Emmer, Michele, Ed. The Visual Mind: Art and Mathematics. Cambridge: MIT Press, 1993. p. 216 |
There were Neolithic solids found in Scotland, and excavations near Padova have unearthed an Etruscan dodecahedron, c. 500 BCE, probably used as a toy.
Kepler
 |
Slide 3-6: Kepler's Model of Universe
Lawlor, p. 106 |
In 1596 Kepler published a tract called The Cosmic Mystery in which he envisioned the universe as consisting of nested Platonic Solids whose inscribed spheres determine the orbits of the planets, all enclosed in a sphere representing the outer heaven. Of course, his observations did not fit this scheme. We'll encounter Kepler again in our unit on Celestial Themes in Art.
Polyhedra and Plagiarism in the Renaissance
 |
Slide 14-10 : JACOPO DE 'BARBERI: Luca Pacioli, c. 1499 |
This painting shows Fra Luca Pacioli and his student, Guidobaldo, Duke of Urbino. In the upper left is a rhombi-cuboctahedron, and on the table is a dodecahedron on top of a copy of Euclid's Elements.
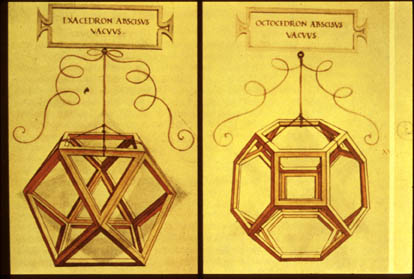 |
Slide 15-11 : Leonardo's Illustrations for Luca's book.
Da Divina Proportione |
Luca Pacioli wrote a book called Da Divina Proportione (1509) which contained a section on the Platonic Solids and other solids, which has 60 plates of solids by none other than his student Leonardo da Vinci. We'll tell the whole story of how this material was stolen from Luca's teacher Piero della Francesca in our unit on Polyhedra and Plagiarism in the Renaissance.
Platonic Solids as Art Motifs
 |
Slide 6-12: UCELLO: Mosaic from San Marco Cathedral,
Venice,1425-1430 plate J2
Emmer, Michele, Ed. The Visual Mind: Art and Mathematics. Cambridge: MIT Press, 1993. |
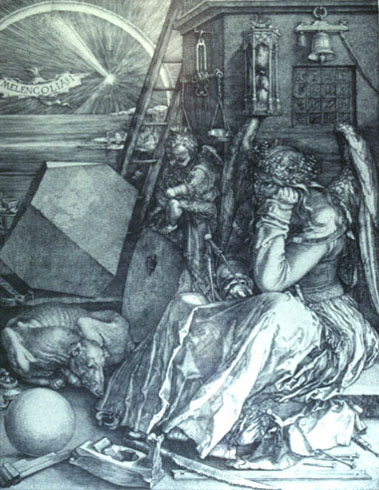 |
Slide 16-08: DURER:
Melancolia I, 1514
citation |
Albrech Durer (1471-1528) had a keen interest in geometry, as we'll see in a later unit. This famous engraving shows an irregular polyhedron, as well as a sphere, a magic square, and compasses. People who have analyzed this polyhedron have decided that its actually a cube with opposite corners cut off.
 |
Slide 6-13: NEUFCHATEL, Nicolaus:
Picture of Johannes Neudorfer and His Son,1561.
Kemp, Martin. Leonardo on Painting. New Haven: Yale U. Press, 1989. p. 63 |
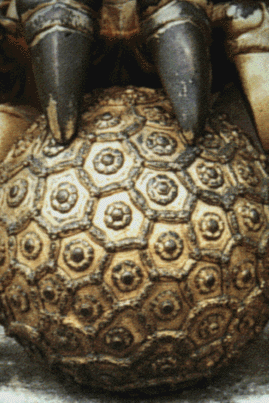 |
Slide 6-14: Gold-plated lion from the front of the Gate of Heavenly Purity,
Closeup of Ball.
Forbidden City, Beijing. From Qing Dynasty (1736-1796) |
This ball has hexagons interspersed with pentagons.
Polyhedra in Art in the Twentieth Century

|
Slides 6-15, 6-16, 6-17:
Giacometti's Works
Hohl, Reinhold. Alberto Giacometti. NY: Abrams, 1972. |
The Swiss artist Alberto Giacometti (1901-1966) often included polyhedra in his earlier surrealist works such as these two drawings and a sculpture.
 |
Slide 21-5:
ESCHER:Stars
1948 (#123) |
We'll talk about M.C. Escher (1902-1972) in detail when we get to the 20th Century, but lets just peek at his 1948 engraving, Stars. Note the similarity between this polyhedron and Leonardo's illustrations for Pacioli's book.
 |
Slide 21-06: Escher
contemplating his nested set of Platonic Solids
citation |
Escher made a set of nested Platonic Solids. When he moved to a new studio he have away most of his belongings but took his beloved model.
Other Twentieth Century artists using polyhedra include Harriet Brisson, Paul Calter, and Lucio Saffaro.
 |
Slide 6-18:Truncated
Close-Packing Octahedra, Rhombidodecahedra, and Cubes.
Plexiglass, aluminum tubes, and nylon cord, 1976
Emmer, Michele, Ed. The Visual Mind: Art and Mathematics. Cambridge: MIT Press, 1993. plate B3 |

|
Slides 6-19, 6-20, 6-21: Platonic Solids
Calter's Sorcerer's Circle |
 |
Slide 6-22: LUCIO SAFFARO:
Platonic Forms. Computer graphic, 1989.
Emmer, Michele, Ed. The Visual Mind: Art and Mathematics. Cambridge: MIT Press, 1993. plate A3 |
Project: Make a work of art featuring polyhedra.
Summary
So we've seen the origins of the Platonic Solids, starting even before Plato, and have briefly traced the influence of the polygons in art right up to the present.
We've also had a first look at some subjects we'll look at in more detail later.
For mathematical topics, we've briefly looked at sequences and series and the geometry of the polyhedra.
Reading Assignment:
Plato, Timaeus, the selection in your reader.
Emmer, The Visual Mind, from your reader
Calter, selection from Technical Mathematics with Calculus, handout
Additional References from your Bibliography :
Wenninger Pedoe Kappraff Irma Richter Lawlor Euclid
Ivins Newman Ghyka Wittkower Critchlow
Project: Repeat Plato's calculations and see if you do indeed get a musical scale.
Make some Archimedian Solids
Make some star polyhedra.
Make a work of art featuring polyhedra




