DISCLAIMER: The following practice exam is intended to give you a
very general idea about the kinds of questions that may appear on the
exam. It should not be regarded as a comprehensive study guide for
the exam. In particular, it is possible that topics not covered on this
practice exam will appear on the exam and that topics covered on this
practice exam will not appear on the exam. You are responsible for all
the topics covered in class.
- Suppose that a given tank has valves that allow fluid to flow in at
a rate proportional to the volume of fluid in the tank and out at a rate
proportional to the square of the volume of fluid in the tank.
- Set up a DE that models this situation (assume
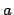 is the constant
of proportionality for the rate of flow into the tank and
is the constant
of proportionality for the rate of flow into the tank and 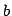 is the
constant of proportionality for the rate of flow out of the tank).
is the
constant of proportionality for the rate of flow out of the tank).
- Draw a slope field for the equation you found above and find the
equilibrium solution(s) if there are any. Describe (in plain English) what
happens to the volume of fluid in the tank as
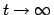 . Be
as specific as you can.
. Be
as specific as you can.
- Assuming there are initially
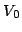 gallons of fluid in the tank,
solve your DE.
gallons of fluid in the tank,
solve your DE.
- Now suppose an extra valve is opened which allows fluid to enter the
tank at a constant rate of
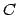 gallons per unit time. Set up a new DE to
model the situation, draw a slope field, and find the equilibrium
solution(s) if there are any.
gallons per unit time. Set up a new DE to
model the situation, draw a slope field, and find the equilibrium
solution(s) if there are any.
- Solve the following differential equations. If no initial
conditions are specified, find the general solution.
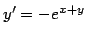
-
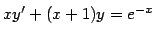 ,
, 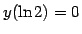
-
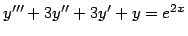
-
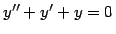 ,
, 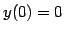 ,
, 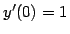
- Find a recursion formula for
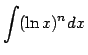 ,
, 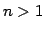 .
.
- Compute the Taylor series for
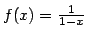 about
about 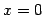 and
find its radius of convergence.
and
find its radius of convergence.
- Compute the Taylor series for
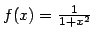 about
about 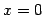 and find its radius of convergence.
and find its radius of convergence.
- Compute the Taylor series for
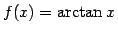 about
about 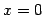 and
find its radius of convergence.
and
find its radius of convergence.
- Explain why the series
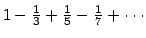 must converge.
must converge.
- It turns out that the above series converges to
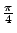 and
thus
and
thus
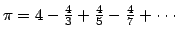 . Explain why this is not a very useful formula for estimating the
numerical value of
. Explain why this is not a very useful formula for estimating the
numerical value of 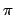 .
.
- Suppose
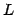 is a linear operator on the space of all differentiable
real-valued functions.
is a linear operator on the space of all differentiable
real-valued functions.
- We can define a linear operator
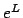 . How? (HINT: how would
Taylor answer this question?)
. How? (HINT: how would
Taylor answer this question?)
- Let
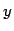 be the function given by
be the function given by 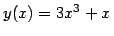 and let
and let 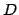 denote
the differential operator. What is
denote
the differential operator. What is 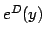 ?
?
Math 9 Fall 2000
2000-10-07
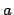 is the constant
of proportionality for the rate of flow into the tank and
is the constant
of proportionality for the rate of flow into the tank and 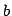 is the
constant of proportionality for the rate of flow out of the tank).
is the
constant of proportionality for the rate of flow out of the tank).
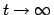 . Be
as specific as you can.
. Be
as specific as you can.
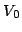 gallons of fluid in the tank,
solve your DE.
gallons of fluid in the tank,
solve your DE.
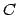 gallons per unit time. Set up a new DE to
model the situation, draw a slope field, and find the equilibrium
solution(s) if there are any.
gallons per unit time. Set up a new DE to
model the situation, draw a slope field, and find the equilibrium
solution(s) if there are any.
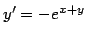
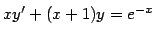 ,
, 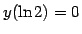
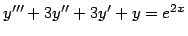
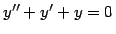 ,
, 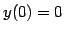 ,
, 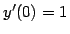
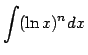 ,
, 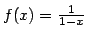 about
about 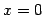 and
find its radius of convergence.
and
find its radius of convergence.
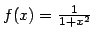 about
about 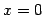 and find its radius of convergence.
and find its radius of convergence.
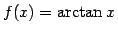 about
about 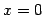 and
find its radius of convergence.
and
find its radius of convergence.
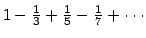 must converge.
must converge.
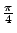 and
thus
and
thus
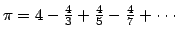 . Explain why this is not a very useful formula for estimating the
numerical value of
. Explain why this is not a very useful formula for estimating the
numerical value of 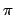 .
.
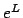 . How? (HINT: how would
Taylor answer this question?)
. How? (HINT: how would
Taylor answer this question?)
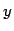 be the function given by
be the function given by 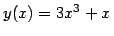 and let
and let 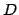 denote
the differential operator. What is
denote
the differential operator. What is 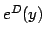 ?
?