

Next: About this document ...
Math 8 Practice Exam Problems
Disclaimer: A few problems from the recent material
- 1.
- Find the general solution to the differential equation
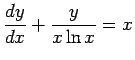 .
.
- 2.
- Find the equation of the tangent plane to the level surface of
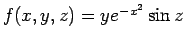 at
at
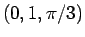 .
.
- 3.
- Suppose that
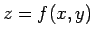 is a smooth real-valued function of two
variables, and that
is a smooth real-valued function of two
variables, and that
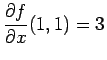 and
and
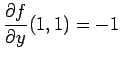 . If
. If 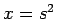 and
and 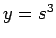 , we may then view
, we may then view 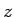 as a function of the single variable
as a function of the single variable 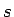 .
The value of
.
The value of
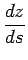 at
at 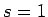 is
is
- 4.
- Find an equation of the curve
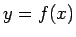 that passes through the
point
that passes through the
point 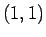 and intersects all level curves of the function
and intersects all level curves of the function
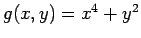 at right angles.
at right angles.
- 5.
- A ball is placed at the point
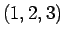 on the surface
on the surface
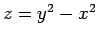 . Give the direction in the
. Give the direction in the  -plane corresponding to the
direction in which the ball will start to roll. Describe the path
in the
-plane corresponding to the
direction in which the ball will start to roll. Describe the path
in the  -plane which the ball will follow. At the point
-plane which the ball will follow. At the point 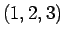 what is the maximum rate at which the ball is descending.
what is the maximum rate at which the ball is descending.
- 6.
- Let
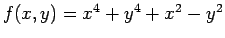 . Find and classify all
critical points of
. Find and classify all
critical points of  . Use the method of Lagrange multipliers to
find the largest and smallest values of
. Use the method of Lagrange multipliers to
find the largest and smallest values of  on the circle
on the circle
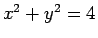 .
.
- 7.
- Consider a function
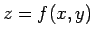 which is defined an has
partial derviatives of all orders for all
which is defined an has
partial derviatives of all orders for all 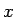 and
and 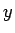 . Suppose the
function
. Suppose the
function 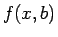 has a local maximum at
has a local maximum at 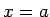 and the function
and the function
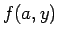 has a local minimum at
has a local minimum at 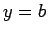 . Can one infer that the point
. Can one infer that the point
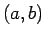 is a critical point, saddle point, local maximum, local
minimum?
is a critical point, saddle point, local maximum, local
minimum?


Next: About this document ...
Math 8 Fall 1999
1999-12-01
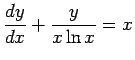 .
.
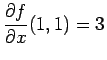 and
and
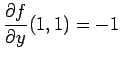 . If
. If 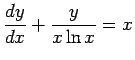 .
.
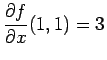 and
and
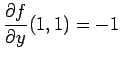 . If
. If