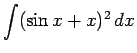 .
.
Solution:
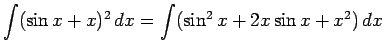 .
.
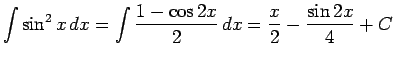 .
.
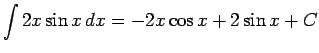 (by parts u = 2x).
(by parts u = 2x).
Putting things togther we get
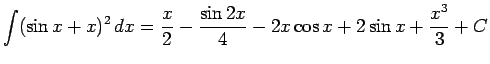 .
.
Solution: The auxilliary equation is
(r-3)4(r2 + 4r + 5)2 which
has real root 3 (with multiplicity 4) and complex conjugate roots
![]() (with multiplicity 2).
(with multiplicity 2).
Thus the general solution will be of the form:
![]() .
.
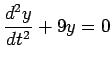 .
Find the general solution as well
as the particular solution which satisfies the initial conditions
y(0) = 3 and y'(0)= 6.
.
Find the general solution as well
as the particular solution which satisfies the initial conditions
y(0) = 3 and y'(0)= 6.
Solution: The auxilliary equation is r2 + 9 = 0 which as roots
![]() .
The general solution has the form
.
The general solution has the form
![]() .
y(0) = 3 implies A = 3.
.
y(0) = 3 implies A = 3.
![]() ,
so
y'(0) = 6 implies B=2, so the particular solution is
,
so
y'(0) = 6 implies B=2, so the particular solution is
![]() .
.
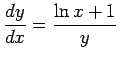 ,
which passes through the point
,
which passes through the point
Solution: This is separable and yields:
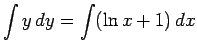 .
Integrating the log by parts
(
.
Integrating the log by parts
(![]() )
yields
)
yields
![]() .
The initial condition
yields C = 4, so the particular solution is
.
The initial condition
yields C = 4, so the particular solution is
![]() .
We note that the solution
.
We note that the solution
![]() passes through
the point
passes through
the point ![]() .
.
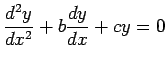 ,
where b and c
are constants and
,
where b and c
are constants and
Solution: The auxilliary equation is
r2 + br + c = 0 which has the
double real root
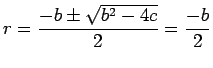 .
.
Thus the general solution is y = C1e-bx/2 + C2xe-bx/2.
Solution: The volume (shells) is given by
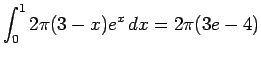 via integration by parts.
via integration by parts.
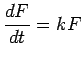 )
If 10 minutes after
walking into an exam, the student remembers only a third of the
formulas initially stored in short-term memory, what fraction of the
formulas are remembered 30 minutes into the exam.
)
If 10 minutes after
walking into an exam, the student remembers only a third of the
formulas initially stored in short-term memory, what fraction of the
formulas are remembered 30 minutes into the exam.
Solution:
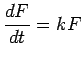 has the general solution
has the general solution
![]() which you can find by separating variables.
F(10) =
F(0)/3 so
which you can find by separating variables.
F(10) =
F(0)/3 so
![]() .
We are assuming F(0) > 0
(hopefully a valid assumption). Then
.
We are assuming F(0) > 0
(hopefully a valid assumption). Then
![]() ,
and
,
and
![]() ,
so
,
so
![]() ,
thus after 30 minutes 1/27th of the formulas are remembered.
,
thus after 30 minutes 1/27th of the formulas are remembered.
Solution:
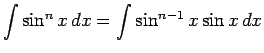 Using
Using
![]() and
and
![]() yields
yields
![]() and
and ![]() .
Integration by parts
yields
.
Integration by parts
yields
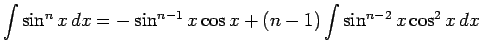 .
.
Since
![]() ,
we substitute to get:
,
we substitute to get:
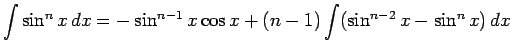 .
.
Shifting the
![]() to the left-hand side, we get:
to the left-hand side, we get:
 ,
or
,
or
