| R | = | 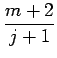 |
|
| = | 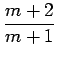 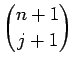 |
||
| = | 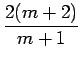 |
Joseph DeStefano
Peter Doyle
J. Laurie Snell
At Emmy's we have a weekly football pool in which each person puts $1 in the pot and picks the winning team in about ten football games. The one who picks the most winners gets the entire pot. A point spread is provided, and the favored team must win by the number of points specified. The effect of the point spread is to make the probability of picking the winner of a particular game approximately 1/2. Joe observed that most of us were just guessing and that some were even tossing a coin to decide which team to pick. He asked if he could contribute $2 to the pot and submit two entries. Joe proposed to submit his choices and those of his evil twin. For each game, his evil twin picks the winner to be the team that Joe picks to lose. This request led to interesting moral, legal, and mathematical discussions and to the following problem.
Assume that all the participants in the football pool except Joe submit one entry and toss a fair coin to make their choices. Joe submits two entries: one for himself and one for his evil twin. For his choices, Joe also tosses a coin. For each game, Joe's evil twin picks as winner the team that Joe picks to lose. The player with the maximum score wins the entire pot. If there is more than one player with the maximum score, the winning players split the pot evenly. Is this a favorable game to Joe? That is, is his expected winning greater than $2?
If Joe and his evil twin are competing only with Dana and there is only one game, the computation is easy. Either Joe or his evil twin will be correct. If Dana is wrong he wins nothing, and if he is correct he shares the $3 pot with either Joe or his evil twin. Thus Dana's expected winning is 3/2×1/2 = 3/4 and Joe's expected winning is 3 - 3/4 = 9/4 = 2.25.
In this trivial situation, Joe has an expected profit of 25 cents. To see if this strategy continues to pay off in a more realistic situation, Joe computed his expected profit while varying the number of players and the number of games. The result is shown in Table 1.
From this computation, Joe noticed that, for a situation typical for our pool, with 10 games and 10 players, his advantage is still significant. In addition, he noticed the surprising fact that, for an odd number of games, the expected profit is independent of the number of games. We now prove this.
Assume that, in addition to Joe and his evil twin,
there are m players tossing coins to choose the
winners for 2n + 1 games. Either Joe or his evil twin must
have more than half correct. Assume that Joe does. Then Joe
will be competing on an equal basis with the subset of other
players who have more than half correct. Thus, if j of the other
players get more than 1/2 correct the expected payment to Joe
is
(m + 2)/(j + 1). The number j is itself a chance quantity
and can be viewed as the number of heads that turn up in m
tosses of a coin. Thus, the expected return R for Joe and his
evil twin is
| R | = | 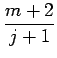 |
|
| = | 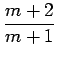 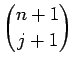 |
||
| = | 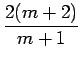 |
Replacing m by x in our expression for R we obtain a corresponding
continuous function. By plotting this function, or by
elementary calculus, one can verify that for x ![]() 1 its
values are greater than 2. It increases to a maximum value
2.345 at x = 2.693 and then decreases approaching 2 as x
goes to infinity. Note from our table that the most advantageous
situation with an expected profit of .344 occurs with five players (m = 3).
1 its
values are greater than 2. It increases to a maximum value
2.345 at x = 2.693 and then decreases approaching 2 as x
goes to infinity. Note from our table that the most advantageous
situation with an expected profit of .344 occurs with five players (m = 3).
A similar argument provides the expected return for the case of an even number of games, but the result is more complicated and not independent of the number of games. For a given number of players the expected return increases to the value for an odd number of games as the number of games tends to infinity. The evil twin strategy poses many other interesting questions. Impressed by the above calculation, Prosser and Snell employ Joe's strategy with Prosser making the picks and Snell playing the role of the evil twin. They have done quite well, but Prosser seems to win more often than Snell. This suggests that Prosser might have a probability greater than 1/2 of picking the winner of a game and raises the question how large this probability must be so that Prosser should reject Snell and play alone. The answer, for the case of 9 games, is that he has only to have a probability of .52 for guessing correctly the team that will win to be better off without the cooperation of Snell when the other players are guessing.
If Prosser and Snell are in collusion and Joe and his evil twin are also entering the pool how much better could these four players do by forming a coalition? More generally, what is the optimal strategy for a group of players that want to form a coalition? This question can be described geometrically as follows: A group of people are picking points at the corners of an n dimensional cube, where n is the number of games, with the objective of getting as close as possible to the choice of a man from Mars, who picks a corner point at random. If m people make their choices at random how should r additional people choose their points to maximize the probability that one of their points is the closest to the point picked by the man from Mars? This geometric interpretation also shows why Joe has an advantage. If you look at the case of three games, so that the points are picked on an ordinary cube, you will notice that Joe and his evil twin pick points on diagonally opposite corners and by so doing have more points near one of their two points than would be true typically for a pair of players who picked their points at random.
We thank our colleagues at Emmy's for many helpful discussions about how to participate in a football pool.
This document was generated using the LaTeX2HTML translator Version 2K.1beta (1.48)
Copyright © 1993, 1994, 1995, 1996,
Nikos Drakos,
Computer Based Learning Unit, University of Leeds.
Copyright © 1997, 1998, 1999,
Ross Moore,
Mathematics Department, Macquarie University, Sydney.
The command line arguments were:
latex2html -html_version 3.2,math,table -reuse 2 -split 0 -info 1 -no_navigation twin
The translation was initiated by Peter G. Doyle on 2003-10-29