


Next: The scaling method in
Up: Solving for the scaling
Previous: Solving for the scaling
Generalized eigenproblem
The problem is solved by a forming a generalized eigenequation,
 |
(6.25) |
which finds the eigenstates of the 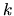 -derivative of tension, treating the
tension quadratic form
-derivative of tension, treating the
tension quadratic form 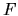 as a norm which is held constant.
The presence of a norm based on the wavefunction at
as a norm which is held constant.
The presence of a norm based on the wavefunction at 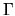 means that null-space vectors can be excluded by the method
of Section 5.3.2 with truncation
means that null-space vectors can be excluded by the method
of Section 5.3.2 with truncation 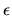 set at about
set at about 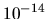 .
It is possible to replace this tension norm
.
It is possible to replace this tension norm 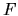 by other norms, for instance
the exact or Dirichlet
by other norms, for instance
the exact or Dirichlet 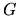 from the previous chapter, however they will not
be quasi-diagonal in the scaling eigenfunction basis. This destroys much of the
benefit of the quasi-diagonality of
from the previous chapter, however they will not
be quasi-diagonal in the scaling eigenfunction basis. This destroys much of the
benefit of the quasi-diagonality of 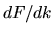 in this basis.
The power of (6.25), as realised by VS,
is that both matrices are quasi-diagonal in this
basis.
Therefore, simultaneous diagonalization (that is, solving the generalized
eigenproblem) of
in this basis.
The power of (6.25), as realised by VS,
is that both matrices are quasi-diagonal in this
basis.
Therefore, simultaneous diagonalization (that is, solving the generalized
eigenproblem) of 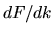 and
and 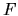 in the computational basis
in the computational basis 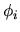 returns a very good approximation to the transformation
returns a very good approximation to the transformation 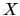 into the
desired eigenfunction basis.
into the
desired eigenfunction basis.
From (6.20) to lowest order the
diagonal elements of 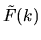 are
are 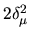 and
those of
and
those of 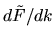 are
are 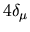 .
The ratio gives the generalized eigenvalue
.
The ratio gives the generalized eigenvalue 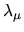 .
The prediction for the eigenwavenumber is
.
The prediction for the eigenwavenumber is
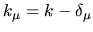 , giving to lowest order (see Section 6.2
for higher orders),
, giving to lowest order (see Section 6.2
for higher orders),
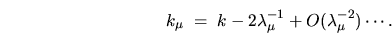 |
(6.26) |
The method will compute all the scaling eigenfunctions
within a wavenumber range of up to about 1, for a system size
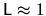 .
This corresponds to whose rescaled boundaries lie within
about
.
This corresponds to whose rescaled boundaries lie within
about 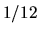 wavelength of the original boundary.
The predicted
wavelength of the original boundary.
The predicted 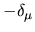 as a function of
as a function of 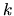 are shown in
Fig. 6.4 (bottom).
are shown in
Fig. 6.4 (bottom).
Figure 6.5:
Comparison of eigenvalue
solutions returned by a single diagonalization of
(6.25) (shown by points, at their resulting 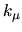 and tensions
and tensions
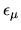 ) against those
obtained by the sweep method of the previous chapter (tension shown by line).
The agreement is excellent (well within the errors of the sweep minima),
apart from the state at
) against those
obtained by the sweep method of the previous chapter (tension shown by line).
The agreement is excellent (well within the errors of the sweep minima),
apart from the state at 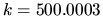 which suffers from error discussed
in Section 6.3.2.
Close eigenvalues not distiguished by the sweep method are
found by the scaling
method, even though the same basis set (500 symmetrized RPWs in the stadium)
was used.
The tensions
which suffers from error discussed
in Section 6.3.2.
Close eigenvalues not distiguished by the sweep method are
found by the scaling
method, even though the same basis set (500 symmetrized RPWs in the stadium)
was used.
The tensions 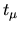 from the scaling method are a factor of 2-3 larger than the
sweep method minima
from the scaling method are a factor of 2-3 larger than the
sweep method minima 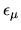 .
.
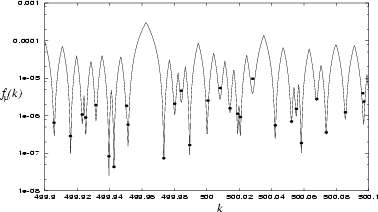 |
Figure 6.6:
Zoom in on Fig. 6.5, with solid line and crosses showing
the sweep and scaling methods respectively (basis of 500 RPWs).
The dotted line and points show the same with an improved basis
(500 RPWs and 30 EPWs).
The scaling method returns 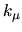 that are well within the `tension rounding
error' width
that are well within the `tension rounding
error' width
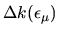 from the sweep method.
The evanescent wave improvement is dramatic, and allows the scaling
from the sweep method.
The evanescent wave improvement is dramatic, and allows the scaling 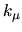 to reach accuracy
to reach accuracy 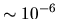 for the
for the 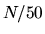 most accurate states.
most accurate states.
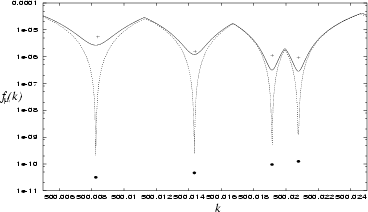 |
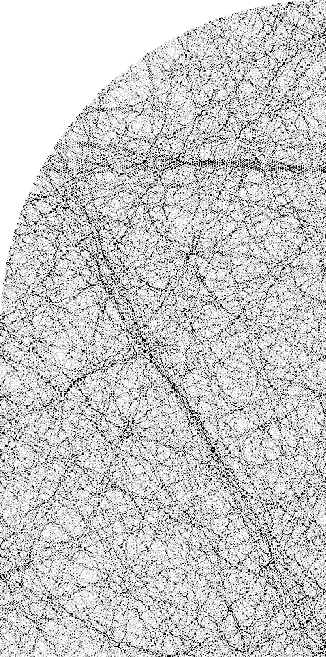
Figure 6.7:
Odd-odd symmetry Dirichlet eigenstate of the 2D stadium billiard
at
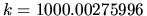 , shown as a probability density plot.
Only the quarter-stadium is shown (spanning about 320 wavelengths).
Scarring by the `bow-tie' orbit is visible.
, shown as a probability density plot.
Only the quarter-stadium is shown (spanning about 320 wavelengths).
Scarring by the `bow-tie' orbit is visible.
 |



Next: The scaling method in
Up: Solving for the scaling
Previous: Solving for the scaling
Alex Barnett
2001-10-03
![]() are
are ![]() and
those of
and
those of ![]() are
are ![]() .
The ratio gives the generalized eigenvalue
.
The ratio gives the generalized eigenvalue ![]() .
The prediction for the eigenwavenumber is
.
The prediction for the eigenwavenumber is
![]() , giving to lowest order (see Section 6.2
for higher orders),
, giving to lowest order (see Section 6.2
for higher orders),


