The classical calculation of Section 2.1 and
the quantum LRT calculation of Section 2.2 gave
the same answers for heating rate.
This is remarkable because the energy evolution
(spreading profile) was different:
the classical spreading is gradual (for
![]() ), whereas the quantum
spreading
involves jumps in units of
), whereas the quantum
spreading
involves jumps in units of ![]() (for driving frequency
(for driving frequency ![]() ).
It is also remarkable because the quantum result is therefore independent
of
).
It is also remarkable because the quantum result is therefore independent
of ![]() .
However the heating rates agree
because the expressions for spreading rate
(second moment of spreading profile) were the same.
The only difference is the replacement of
the classical definition of
.
However the heating rates agree
because the expressions for spreading rate
(second moment of spreading profile) were the same.
The only difference is the replacement of
the classical definition of
![]() by the corresponding
quantum-mechanical definition
by the corresponding
quantum-mechanical definition
![]() .
If these two agree, then there is quantum-classical correspondence (QCC)
as far as dissipation (friction
.
If these two agree, then there is quantum-classical correspondence (QCC)
as far as dissipation (friction ![]() ) is concerned [47,46].
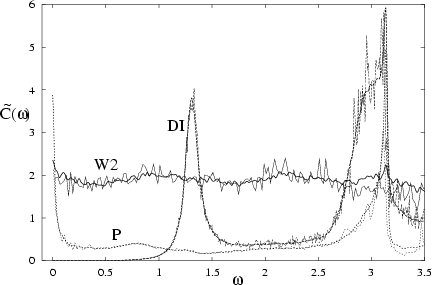
Cohen calls this `restricted correspondence' because of the different
spreading profiles.
Here I present numerical
evidence supporting this claim of QCC in a real system (a 2D cavity).
Hence in the following chapters I will
move freely between the quantum and classical pictures.
In particular, the term `band profile'
will then refer to both quantum and classical
) is concerned [47,46].
Cohen calls this `restricted correspondence' because of the different
spreading profiles.
Here I present numerical
evidence supporting this claim of QCC in a real system (a 2D cavity).
Hence in the following chapters I will
move freely between the quantum and classical pictures.
In particular, the term `band profile'
will then refer to both quantum and classical
![]() auto-correlation spectra.
auto-correlation spectra.
First I briefly mention QCC outside the LRT regime (whose limits
were outlined in the previous
section).
For extremely small ![]() in the quantum-adiabatic regime, there is no
QCC expected because the level spacing distribution
in the quantum-adiabatic regime, there is no
QCC expected because the level spacing distribution ![]() for small
for small
![]() dominates the heating rate [200].
This is a purely quantum effect (determined by certain quantum symmetries
[35,146]), and has no reason to agree
with any classical quantity.
At the other extreme,
as
dominates the heating rate [200].
This is a purely quantum effect (determined by certain quantum symmetries
[35,146]), and has no reason to agree
with any classical quantity.
At the other extreme,
as
![]() the maximum
the maximum ![]() where LRT is valid also vanishes.
Therefore if one is to have QCC in the semiclassical limit
(a fundamental requirement of quantum mechanics being that it reduces to
classical mechanics in this limit),
some new mechanism is required.
As explained by Cohen[47,46], in this limit QCC is achieved
through semiclassical agreement of the spreading profiles
(`detailed correspondence').
where LRT is valid also vanishes.
Therefore if one is to have QCC in the semiclassical limit
(a fundamental requirement of quantum mechanics being that it reduces to
classical mechanics in this limit),
some new mechanism is required.
As explained by Cohen[47,46], in this limit QCC is achieved
through semiclassical agreement of the spreading profiles
(`detailed correspondence').
 |
 |