


Next: Regime of applicability of
Up: Review of the linear
Previous: Heating rate example non-interacting
Relation to susceptibility
Here, for the sake of intuition, I briefly make contact with the traditional
LRT notation arising in condensed matter physics
[127,122,160,99,65].
I consider first the `response' (time-dependent expectation value)
of a general measurable whose operator is 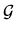 .
Looking at Eq.(2.40) we can write
.
Looking at Eq.(2.40) we can write
![\begin{displaymath}
\langle {\mathcal{G}}(t) \rangle \; = \; {\mathcal{G}}_{mm}...
...} \left[ a_n^* (t) {\mathcal{G}}_{nm}(t) + \mbox{c.c.} \right]
\end{displaymath}](img340.gif) |
(2.54) |
where the first term is the constant
equilibrium value
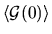 and the other terms
have been kept only up to first order in the driving
and the other terms
have been kept only up to first order in the driving 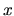 .
The response is linear
but is not generally local in time, i.e. it has memory.
However, because of translational invariance in time, the response must be
local in frequency.
So we can relate the Fourier transform of response to that of driving by
.
The response is linear
but is not generally local in time, i.e. it has memory.
However, because of translational invariance in time, the response must be
local in frequency.
So we can relate the Fourier transform of response to that of driving by
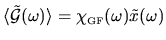 , where
, where
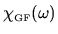 is a generalized susceptibility.
Numerous symmetry relations of
is a generalized susceptibility.
Numerous symmetry relations of
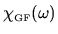 follow from
causality[127]; in particular
follow from
causality[127]; in particular
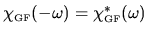 .
Substitution of (2.40) gives
.
Substitution of (2.40) gives
![\begin{displaymath}
\chi_{{\mbox{\tiny GF}}}(\omega) = \frac{i}{\hbar} \int_0^{...
...langle [ {\mathcal{G}}(t), {\mathcal{F}}(0) ]
\right\rangle ,
\end{displaymath}](img345.gif) |
(2.55) |
where the latter form is averaged over  with the appropriate
initial distribution
with the appropriate
initial distribution 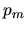 , and is a standard
result of LRT [65].
, and is a standard
result of LRT [65].
We now choose
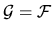 whereupon the subscript
whereupon the subscript
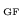 is
no longer needed.
The susceptibility is split into real and imaginary parts,
is
no longer needed.
The susceptibility is split into real and imaginary parts,
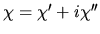 .
The dissipation (energy absorption) is determined by
.
The dissipation (energy absorption) is determined by 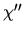 [127],
since, using the driving (2.41) we have
[127],
since, using the driving (2.41) we have
where at the last stage the oscillatory terms average to zero.
This heating rate expression results entirely from the definition of 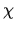 .
However now our friction coefficient from the previous section
can be seen to be simply
.
However now our friction coefficient from the previous section
can be seen to be simply
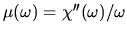 .
.
We should also note that in the condensed matter physics context
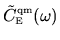 is proportional to the dynamic form factor
is proportional to the dynamic form factor
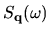 if we associate
if we associate
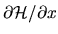 with the density operator
of a mode labelled
with the density operator
of a mode labelled 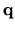 [160].
In the case where
[160].
In the case where 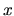 is flux enclosed by a mesoscopic sample (quantum dot),
is flux enclosed by a mesoscopic sample (quantum dot),
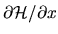 is a current operator, thus
is a current operator, thus 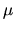 determines the conductivity of the system.
As one would expect, the conductivity is then given by the
time-integral of the current-current
correlation
determines the conductivity of the system.
As one would expect, the conductivity is then given by the
time-integral of the current-current
correlation
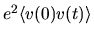 [122,99,8].
We have performed such a calculation for a chaotic mesoscopic dot
[15].
[122,99,8].
We have performed such a calculation for a chaotic mesoscopic dot
[15].



Next: Regime of applicability of
Up: Review of the linear
Previous: Heating rate example non-interacting
Alex Barnett
2001-10-03
![]() .
Looking at Eq.(2.40) we can write
.
Looking at Eq.(2.40) we can write
![]() whereupon the subscript
whereupon the subscript
![]() is
no longer needed.
The susceptibility is split into real and imaginary parts,
is
no longer needed.
The susceptibility is split into real and imaginary parts,
![]() .
The dissipation (energy absorption) is determined by
.
The dissipation (energy absorption) is determined by ![]() [127],
since, using the driving (2.41) we have
[127],
since, using the driving (2.41) we have
![]() is proportional to the dynamic form factor
is proportional to the dynamic form factor
![]() if we associate
if we associate
![]() with the density operator
of a mode labelled
with the density operator
of a mode labelled ![]() [160].
In the case where
[160].
In the case where ![]() is flux enclosed by a mesoscopic sample (quantum dot),
is flux enclosed by a mesoscopic sample (quantum dot),
![]() is a current operator, thus
is a current operator, thus ![]() determines the conductivity of the system.
As one would expect, the conductivity is then given by the
time-integral of the current-current
correlation
determines the conductivity of the system.
As one would expect, the conductivity is then given by the
time-integral of the current-current
correlation
![]() [122,99,8].
We have performed such a calculation for a chaotic mesoscopic dot
[15].
[122,99,8].
We have performed such a calculation for a chaotic mesoscopic dot
[15].